
Talaan ng mga Nilalaman:
- Hakbang 1: Pag-install ng Library
- Hakbang 2: Fourier Transform at FFT Concepts
- Hakbang 3: Simulate a Signal
- Hakbang 4: Pagsusuri ng isang Simulated Signal - Coding
- Hakbang 5: Pagsusuri ng isang Simulated Signal - Mga Resulta
- Hakbang 6: Pagsusuri ng isang Tunay na Signal - Pag-kable ng ADC
- Hakbang 7: Pagsusuri ng isang Tunay na Signal - Coding
- Hakbang 8: Pagsusuri ng isang Tunay na Signal - Mga Resulta
- Hakbang 9: Paano Tungkol sa isang Clipped Sinusoidal Signal?
- May -akda John Day day@howwhatproduce.com.
- Public 2024-01-30 13:11.
- Huling binago 2025-06-01 06:10.


Ang medyo madaling tutorial na ito (isinasaalang-alang ang pagiging kumplikado ng paksang ito) ay ipapakita sa iyo kung paano ka makagagawa ng isang napaka-simpleng 1024 mga sample ng spectrum analyzer gamit ang isang Arduino type board (1284 Makitid) at ang serial plotter. Anumang uri ng board na katugmang Arduino ay gagawin, ngunit mas maraming RAM ang mayroon ito, ang pinakamahusay na resolusyon ng dalas na makukuha mo. Mangangailangan ito ng higit sa 8 KB ng RAM upang makalkula ang FFT na may 1024 na mga sample.
Ginagamit ang pagsusuri ng Spectrum upang matukoy ang pangunahing mga bahagi ng dalas ng isang senyas. Maraming mga tunog (tulad ng mga ginawa ng isang instrumentong pangmusika) ay binubuo ng isang pangunahing dalas at ilang mga harmonika na may dalas na isang integer na maramihang ng pangunahing dalas. Ipapakita sa iyo ng spectrum analyzer ang lahat ng mga sangkap na parang multo.
Maaaring gusto mong gamitin ang setup na ito bilang isang counter ng dalas o upang suriin ang anumang uri ng mga senyas na pinaghihinalaan mong nagdadala ng ingay sa iyong elektronikong circuit.
Magtutuon kami dito sa bahagi ng software. Kung nais mong gumawa ng isang permanenteng circuit para sa isang tukoy na aplikasyon kakailanganin mong palakasin at salain ang signal. Ang pre-conditioning na ito ay ganap na nakasalalay sa signal na gusto mong pag-aralan, depende sa amplitude, impedance, maximum frequency atbp … Maaari mong suriin ang
Hakbang 1: Pag-install ng Library
Gagamitin namin ang ArduinoFFT library na isinulat ni Enrique Condes. Dahil nais naming magtipid ng RAM hangga't maaari ay gagamitin namin ang pagbuo ng sangay ng imbakan na ito na nagpapahintulot na gamitin ang uri ng float data (sa halip na doble) upang maiimbak ang na-sample at na-compute na data. Kaya kailangan naming i-install ito nang manu-mano. Huwag magalala, i-download lamang ang archive at i-compress ito sa iyong folder ng library ng Arduino (halimbawa sa default na pagsasaayos ng Windows 10: C: / Users / _your_user_name_ / Documents / Arduino / libraries)
Maaari mong suriin na ang aklatan ay na-install nang tama sa pamamagitan ng pag-iipon ng isa sa mga halimbawang ibinigay, tulad ng "FFT_01.ino."
Hakbang 2: Fourier Transform at FFT Concepts
Babala: kung hindi mo matiis ang nakakakita ng anumang notasyong matematika baka gusto mong laktawan ang Hakbang 3. Gayunpaman, kung hindi mo makuha ang lahat, isaalang-alang lamang ang pagtatapos sa dulo ng seksyon.
Ang frequency spectrum ay nakuha sa pamamagitan ng isang Fast Fourier Transform algorithm. Ang FFT ay isang digital na pagpapatupad na tinatayang ang konsepto ng matematika ng Fourier Transform. Sa ilalim ng konseptong ito sa sandaling makuha mo ang ebolusyon ng isang senyas kasunod ng isang axis ng oras, malalaman mo ang representasyon nito sa isang domain ng dalas, na binubuo ng mga kumplikadong (totoong + haka-haka) na mga halaga. Ang konsepto ay katumbasan, kaya kapag alam mo ang representasyon ng dalas ng domain maaari mo itong ibalik sa time domain at ibalik ang signal nang eksakto tulad ng bago ang pagbago.
Ngunit ano ang gagawin natin sa hanay ng na-compute na kumplikadong mga halaga sa domain ng oras? Kaya, karamihan sa mga ito ay maiiwan sa mga inhinyero. Para sa amin tatawag kami ng isa pang algorithm na ibabago ang mga kumplikadong halagang ito sa data ng spectral density: iyon ay isang halaga ng lakas (= intensity) na nauugnay sa bawat frequency band. Ang bilang ng frequency band ay magiging pareho sa bilang ng mga sample.
Tiyak na pamilyar ka sa konsepto ng pangbalanse, tulad ng isang ito Bumalik sa 1980s Gamit ang Graphic EQ. Sa gayon, makakakuha kami ng parehong uri ng mga resulta ngunit may 1024 mga banda sa halip na 16 at higit na higit na resolusyon sa kasidhian. Kapag ang pangbalanse ay nagbibigay ng isang pandaigdigang pagtingin sa musika, pinapayagan ng pinong pagtatasa ng parang multo na tumpak na makalkula ang tindi ng bawat isa sa 1024 na banda.
Isang perpektong konsepto, ngunit:
- Dahil ang FFT ay isang digitalized na bersyon ng Fourier transform, tinatantiya nito ang digital signal, at tinatanggal ang ilang impormasyon. Kaya, mahigpit na nagsasalita, ang resulta ng FFT kung binago pabalik gamit ang isang baligtad na FFT algorithm ay hindi magbibigay ng eksaktong orihinal na signal.
- Gayundin ang teorya ay isinasaalang-alang ang isang senyas na hindi may hangganan, ngunit iyon ay isang pangmatagalang palaging signal. Dahil ise-digital namin ito para lamang sa isang tiyak na tagal ng oras (hal. Mga sample), ilang mga error pa ang ipapakilala.
-
Sa wakas ang resolusyon ng analog sa digital na conversion ay makakaapekto sa kalidad ng na-compute na mga halaga.
Sa pagsasanay
1) Ang dalas ng sampling (nabanggit na fs)
Sisimulan namin ang isang senyas, ibig sabihin, susukatin ang amplitude nito, bawat 1 / fs segundo. fs ay ang dalas ng sampling. Halimbawa kung sample namin sa 8 KHz, ang ADC (analog sa digital converter) na onboard ng chip ay magbibigay ng isang pagsukat tuwing 1/8000 ng mga segundo.
2) Ang bilang ng mga sample (nabanggit N o mga sample sa code)
Dahil kailangan naming makuha ang lahat ng mga halaga bago patakbuhin ang FFT kakailanganin nating iimbak ang mga ito at sa gayon ay lilimitahan natin ang bilang ng mga sample. Ang FFT algorithm ay nangangailangan ng isang bilang ng mga sample na isang lakas ng 2. Ang mas maraming mga sample na mayroon kaming mas mahusay ngunit ito ay tumatagal ng isang pulutong ng memorya, higit sa lahat na kakailanganin din namin upang iimbak ang binago data, na ang mga kumplikadong halaga. Ang Arduino FFT library ay nakakatipid ng ilang puwang sa pamamagitan ng paggamit
- Ang isang array na pinangalanang "vReal" upang maiimbak ang naka-sample na data at pagkatapos ay ang totoong bahagi ng binago na data
- Ang isang array na pinangalanang "vImag" upang maiimbak ang haka-haka na bahagi ng nabago na data
Ang kinakailangang halaga ng RAM ay katumbas ng 2 (arrays) * 32 (bits) * N (mga sample).
Kaya sa aming Atmega1284 na mayroong magandang 16 KB ng RAM ay mag-iimbak kami ng maximum na N = 16000 * 8/64 = 2000 na mga halaga. Dahil ang bilang ng mga halaga ay dapat na isang lakas ng 2, mag-iimbak kami ng maximum na 1024 na mga halaga.
3) Ang resolusyon ng dalas
Ang FFT ay makalkula ang mga halaga para sa maraming mga banda ng dalas ng bilang ng mga sample. Ang mga banda na ito ay mula sa 0 HZ hanggang sa dalas ng sampling (fs). Samakatuwid, ang resolusyon ng dalas ay:
Fresolution = fs / N
Ang resolusyon ay mas mahusay kapag mas mababa. Kaya para sa mas mahusay na resolusyon (mas mababa) na gusto namin:
- higit pang mga sample, at / o
- isang mas mababang fs
Ngunit …
4) Minimal fs
Dahil nais naming makita ang maraming mga frequency, ang ilan sa mga ito ay mas mataas kaysa sa "pangunahing dalas" na hindi namin maitakda ang fs masyadong mababa. Sa katunayan mayroong tequem ng pag-sample ng Nyquist - Shannon na pinipilit kaming magkaroon ng dalas ng sampling nang higit sa dalawang beses ang maximum na dalas na nais naming subukan.
Halimbawa Sa katunayan madalas itinakda ito ng mga elektroniks sa 2.5 (o kahit 2.52) * ang maximum na dalas. Sa halimbawang ito ay magiging 2.5 * 15 KHz = 37.5 KHz. Kadalasang mga frequency ng sampling sa propesyonal na audio ay 44.1 KHz (audio CD recording), 48 KHz at higit pa.
Konklusyon:
Ang mga puntos na 1 hanggang 4 ay humantong sa: nais naming gumamit ng maraming mga sample hangga't maaari. Sa aming kaso sa isang 16 KB ng aparato ng RAM isasaalang-alang namin ang 1024 na mga sample. Nais naming sample sa pinakamababang dalas ng sampling hangga't maaari, basta sapat na mataas upang masuri ang pinakamataas na dalas na inaasahan namin sa aming signal (2.5 * ang dalas na ito, hindi bababa sa).
Hakbang 3: Simulate a Signal

Para sa aming unang pagsubok, babaguhin namin nang bahagya ang halimbawang TFT_01.ino na ibinigay sa library, upang pag-aralan ang isang senyas na binubuo ng
- Ang pangunahing dalas, nakatakda sa 440 Hz (musikal A)
- Ika-3 maharmonya sa kalahati ng lakas ng pangunahing ("-3 dB")
- Ika-5 maharmonya sa 1/4 ng lakas ng pangunahing ("-6 dB)
Maaari mong makita sa larawan sa itaas ang nagresultang signal. Tila talagang isang tunay na senyas na kung minsan ay makikita ang isang oscilloscope (tatawagin kong "Batman") sa sitwasyon kapag mayroong isang pag-clipping ng isang sinusoidal signal.
Hakbang 4: Pagsusuri ng isang Simulated Signal - Coding
0) Isama ang library
# isama ang "arduinoFFT.h"
1) Mga Kahulugan
Sa mga seksyon ng mga pagdedeklara, mayroon kaming
const byte adcPin = 0; // A0
mga halimbawa ng uint16_t = 1024; // Ang halagang ito ay DAPAT palaging isang kapangyarihan ng 2 const uint16_t samplingFrequency = 8000; // Makakaapekto sa halaga ng timer max sa timer_setup () SYSCLOCK / 8 / samplingFrequency ay dapat na isang integer
Dahil ang signal ay may isang 5th harmonics (dalas ng maharmonya na ito = 5 * 440 = 2200 Hz) kailangan naming itakda ang dalas ng sampling sa itaas 2.5 * 2200 = 5500 Hz. Dito pinili ko ang 8000 Hz.
Idineklara din namin ang mga array kung saan iimbak namin ang hilaw at na-compute na data
float vReal [mga sample];
float vImag [mga sample];
2) Instantiation
Lumilikha kami ng isang object ng ArduinoFFT. Ang bersyon ng dev ng ArduinoFFT ay gumagamit ng isang template upang maaari naming magamit ang alinman sa float o ang dobleng uri ng data. Ang Float (32 bits) ay sapat na patungkol sa pangkalahatang katumpakan ng aming programa.
ArduinoFFT FFT = ArduinoFFT (vReal, vImag, mga sample, samplingFrequency);
3) Simulate ang signal sa pamamagitan ng pag-populate ng vReal array, sa halip na ipunan ito ng mga halaga ng ADC.
Sa simula ng Loop pinupunan namin ang vReal array na may:
float cycle = ((((mga halimbawa) * signalFrequency) / samplingFrequency); // Bilang ng mga cycle ng signal na babasahin ang sampling
para sa (uint16_t i = 0; i <sampol; i ++) {vReal = float ((amplitude * (sin ((i * (TWO_PI * cycle)) / sample)))); / * Bumuo ng data na may positibo at mga negatibong halagang * / vReal + = float ((amplitude * (sin ((3 * i * (Two_PI * cycle)) / sample)) / 2.0); / * Bumuo ng data na may positibo at negatibong halagang * / vReal + = float ((amplitude * (sin ((5 * i * (Two_PI * cycle)) / sample))) / 4.0); / * Bumuo ng data na may positibo at negatibong mga halaga * / vImag = 0.0; // Ang haka-haka na bahagi ay dapat na zero sa kaso ng pag-ikot upang maiwasan ang maling pagkalkula at pag-apaw}
Nagdagdag kami ng isang digitalisasyon ng pangunahing alon at ang dalawang harmonika na may mas kaunting amplitude. Kaysa ipasimuno namin ang haka-haka na hanay na may mga zero. Dahil ang array na ito ay pinunan ng FFT algorithm kailangan namin itong i-clear muli bago ang bawat bagong pagkalkula.
4) FFT computing
Pagkatapos makalkula namin ang FFT at ang density ng parang multo
FFT.windowing (FFTWindow:: Hamming, FFTDirection:: Forward);
FFT.compute (FFTDirection:: Ipasa); / * Compute FFT * / FFT.complexToMagnitude (); / * Compute magnitude * /
Binabago ng operasyon ng FFT.windowing (…) ang hilaw na data dahil pinatakbo namin ang FFT sa isang limitadong bilang ng mga sample. Ang una at huling mga sample ay nagpapakita ng isang paghinto (mayroong "wala" sa isa sa kanilang panig). Ito ay isang mapagkukunan ng error. Ang operasyon ng "windowing" ay may kaugaliang mabawasan ang error na ito.
Ang FFT.compute (…) na may direksyon na "Forward" ay kinukwenta ang pagbabago mula sa time domain hanggang sa domain ng dalas.
Pagkatapos ay kinukuwenta namin ang mga halaga ng lakas (ibig sabihin, intensity) para sa bawat isa sa mga frequency band. Ang vReal array ay napuno na ngayon ng mga halaga ng magnitude.
5) Serial plotter drawing
I-print natin ang mga halaga sa serial plotter sa pamamagitan ng pagtawag sa function na printVector (…)
PrintVector (vReal, (mga halimbawa >> 1), SCL_FREQUENCY);
Ito ay isang pangkaraniwang pag-andar na nagbibigay-daan upang mag-print ng data gamit ang isang axis ng oras o isang dalas na axis.
Nagpi-print din kami ng dalas ng banda na may pinakamataas na halaga ng magnitude
float x = FFT.majorPeak ();
Serial.print ("f0 ="); Serial.print (x, 6); Serial.println ("Hz");
Hakbang 5: Pagsusuri ng isang Simulated Signal - Mga Resulta

Nakikita namin ang 3 mga spike na naaayon sa pangunahing dalas (f0), ang ika-3 at ika-5 na mga pagsasabay, na may kalahati at 1 / ika-4 ng lakas na f0, tulad ng inaasahan. Maaari nating basahin sa tuktok ng window f0 = 440.430114 Hz. Ang halagang ito ay hindi eksaktong 440 Hz, dahil sa lahat ng mga kadahilanang ipinaliwanag sa itaas, ngunit malapit ito sa totoong halaga. Hindi talaga kinakailangan na magpakita ng maraming hindi gaanong decimal.
Hakbang 6: Pagsusuri ng isang Tunay na Signal - Pag-kable ng ADC

Dahil alam namin kung paano magpatuloy sa teorya, nais naming pag-aralan ang isang tunay na signal.
Ang mga kable ay napaka-simple. Ikonekta ang mga bakuran nang magkasama at ang linya ng signal sa A0 pin ng iyong board sa pamamagitan ng isang resistor ng serye na may halagang 1 KOhm hanggang 10 KOhm.
Protektahan ng resistor ng serye ang analog input at maiiwasang mag-ring. Dapat itong kasing taas hangga't maaari upang maiwasan ang pag-ring, at bilang mababang hangga't maaari upang makapagbigay ng sapat na kasalukuyang upang mabilis na singilin ang ADC. Sumangguni sa MCU datasheet upang malaman ang inaasahang impedance ng signal na konektado sa input ng ADC.
Para sa demo na ito, gumamit ako ng isang generator ng pagpapaandar upang pakainin ang isang sinusoidal signal ng dalas na 440 Hz at amplitude sa paligid ng 5 volts (mas mabuti kung ang amplitude ay nasa pagitan ng 3 at 5 volts kaya ang ADC ay ginagamit malapit sa buong sukat), sa pamamagitan ng isang resistor na 1.2 KOhm.
Hakbang 7: Pagsusuri ng isang Tunay na Signal - Coding
0) Isama ang library
# isama ang "arduinoFFT.h"
1) Mga deklarasyon at instanciation
Sa seksyon ng deklarasyon tinutukoy namin ang input ng ADC (A0), ang bilang ng mga sample at dalas ng sampling, tulad ng nakaraang halimbawa.
const byte adcPin = 0; // A0
mga halimbawa ng uint16_t = 1024; // Ang halagang ito ay DAPAT palaging isang kapangyarihan ng 2 const uint16_t samplingFrequency = 8000; // Makakaapekto sa halaga ng timer max sa timer_setup () SYSCLOCK / 8 / samplingFrequency ay dapat na isang integer
Lumilikha kami ng object ng ArduinoFFT
ArduinoFFT FFT = ArduinoFFT (vReal, vImag, mga sample, samplingFrequency);
2) Pag-setup ng timer at ADC
Itinakda namin ang timer 1 kaya't umikot ito sa dalas ng sampling (8 KHz) at nagtataas ng isang nakakagambala sa paghahambing ng output.
void timer_setup () {
// reset Timer 1 TCCR1A = 0; TCCR1B = 0; TCNT1 = 0; TCCR1B = bit (CS11) | bit (WGM12); // CTC, prescaler ng 8 TIMSK1 = bit (OCIE1B); OCR1A = (((16000000/8) / samplingFrequency) -1; }
At itakda ang ADC sa gayon ito
- Gumagamit ng A0 bilang input
- Awtomatikong nag-trigger ang bawat output ng 1 sa paghahambing ng tugma B
- Bumubuo ng isang nakakagambala kapag nakumpleto ang conversion
Ang ADC na orasan ay nakatakda sa 1 MHz, sa pamamagitan ng prescaling ng system clock (16 MHz) ng 16. Dahil ang bawat conversion ay tumatagal ng humigit-kumulang13 na mga orasan sa buong sukat, ang mga conversion ay maaaring makamit sa dalas na 1/13 = 0.076 MHz = 76 KHz. Ang dalas ng sampling ay dapat na makabuluhang mas mababa sa 76 KHz upang hayaan ang ADC na magkaroon ng oras upang mai-sample ang data. (pinili namin ang fs = 8 KHz).
void adc_setup () {
ADCSRA = bit (ADEN) | bit (ADIE) | bit (ADIF); // turn ADC on, want interrupt sa pagkumpleto ng ADCSRA | = bit (ADPS2); // Prescaler ng 16 ADMUX = bit (REFS0) | (adcPin & 7); // setting the ADC input ADCSRB = bit (ADTS0) | bit (ADTS2); // Timer / Counter1 Paghambingin ang mapagkukunang trigger ng Match B na ADCSRA | = bit (ADATE); // i-on ang awtomatikong pag-trigger}
Idineklara namin ang nagagambala na handler na tatawagin pagkatapos ng bawat pag-convert ng ADC upang maiimbak ang na-convert na data sa vReal array, at i-clear ang makagambala
// ADC kumpletong ISR
ISR (ADC_vect) {vReal [resultNumber ++] = ADC; kung (resultaNumber == mga sample) {ADCSRA = 0; // i-off ang ADC}} EMPTY_INTERRUPT (TIMER1_COMPB_vect);
Maaari kang magkaroon ng isang lubusang paliwanag sa pag-convert ng ADC sa Arduino (analogRead).
3) Pag-setup
Sa pag-andar ng pag-setup ay nililinaw namin ang talahanayan ng haka-haka na data at tawagan ang mga pagpapaandar ng timer at ADC
zeroI (); // isang pagpapaandar na itinakda sa 0 lahat ng haka-haka na data - ipinaliwanag sa nakaraang seksyon
timer_setup (); adc_setup ();
3) Loop
FFT.dcRemoval (); // Tanggalin ang bahagi ng DC ng signal na ito dahil ang ADC ay na-refer sa lupa
FFT.windowing (FFTWindow:: Hamming, FFTDirection:: Forward); // Timbangin ang data FFT.compute (FFTDirection:: Ipasa); // Compute FFT FFT.complexToMagnitude (); // Compute magnitude // pag-print ng spectrum at ang pangunahing dalas f0 PrintVector (vReal, (mga sample >> 1), SCL_FREQUENCY); float x = FFT.majorPeak (); Serial.print ("f0 ="); Serial.print (x, 6); Serial.println ("Hz");
Inaalis namin ang bahagi ng DC dahil ang ADC ay isinangguni sa lupa at ang signal ay nakasentro sa paligid ng 2.5 volts na tinatayang.
Pagkatapos ay kinukuwenta namin ang data tulad ng ipinaliwanag sa nakaraang halimbawa.
Hakbang 8: Pagsusuri ng isang Tunay na Signal - Mga Resulta

Sa katunayan nakikita lamang namin ang isang dalas sa simpleng signal na ito. Ang nakalkula na pangunahing dalas ay 440.118194 Hz. Narito muli ang halaga ay isang napakalapit na approximation ng tunay na dalas.
Hakbang 9: Paano Tungkol sa isang Clipped Sinusoidal Signal?

Hinahayaan ngayong mag-overdrive ng kaunti ang ADC sa pamamagitan ng pagtaas ng amplitude ng signal sa itaas ng 5 volts, kaya't ito ay na-clip. Huwag itulak masyadong mush hindi upang sirain ang input ng ADC!
Maaari naming makita ang ilang mga harmonika na lumilitaw. Ang pag-clip ng signal ay lumilikha ng mga bahagi ng mataas na dalas.
Nakita mo ang mga batayan ng pagtatasa ng FFT sa isang Arduino board. Ngayon ay maaari mong subukang baguhin ang dalas ng sampling, ang bilang ng mga sample at ang parameter ng windowing. Nagdadagdag din ang library ng ilang parameter upang makalkula ang FFT nang mas mabilis na may hindi gaanong katumpakan. Mapapansin mo na kung itinakda mo ang dalas ng sampling ng masyadong mababa, ang nakakalkula na magnitude ay lilitaw na lubos na nagkakamali dahil sa spectral natitiklop.
Inirerekumendang:
Paano Gumawa ng isang LED Audio Spectrum Analyzer: 7 Mga Hakbang (na may Mga Larawan)

Paano Gumawa ng isang LED Audio Spectrum Analyzer: Ang LED Audio Spectrum Analyzer ay bumubuo ng magandang pattern ng pag-iilaw ayon sa tindi ng musika. Maraming mga DIY LED Music Spectrum kit na magagamit sa merkado, ngunit dito kami gagawa ng isang LED Audio Spectrum Ang Analyzer ay gumagamit ng NeoPixe
DIY FFT Audio Spectrum Analyzer: 3 Mga Hakbang

DIY FFT Audio Spectrum Analyzer: Ang FFT spectrum analyzer ay isang kagamitan sa pagsubok na gumagamit ng Fourier analysis at digital diskarte sa pagpoproseso ng signal upang magbigay ng pagsusuri sa spectrum. Paggamit ng Fourier analysis posible para sa isang halaga sa, halimbawa, ang patuloy na domain ng oras na maging
Sample Pad Controller Paggamit ng Purong Data: 4 Mga Hakbang
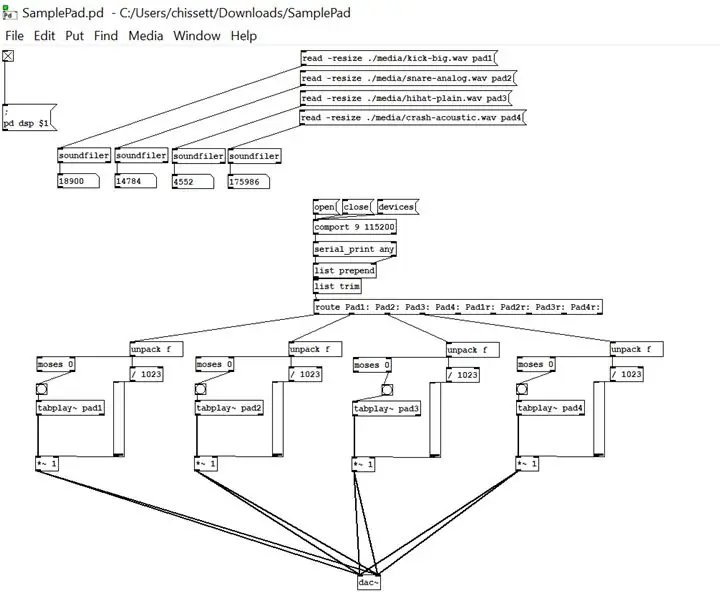
Sample Pad Controller Paggamit ng Purong Data: Sa Instructable na ito, lilikha ako ng isang tagapamahala upang payagan ang ilang mga lumang Roland electronic drum kit pads na magpalitaw ng mga tunog nang walang orihinal na module ng drum na kasama ng kit. Gagamitin ko ang Pure Data upang lumikha ng isang patch upang mai-load ilang mga wav file at pagkatapos ay p
Rock Sample Analyzer: 4 na Hakbang

Rock Sample Analyzer: Ang Rock Sample Analyzer ay ginagamit upang makilala at pag-aralan ang mga uri ng mga sample ng mga bato gamit ang malambot na diskarte sa panginginig ng boses. Ito ay isang pamamaraang nobela sa pagkilala sa mga sample ng bato. Kung ang isang meteorite o anumang hindi kilalang sample ng bato ay naroroon, maaaring matantya ng isang
Paggamit ng isang RTA Program Bilang isang Oscilloscope o Circuit Analyzer: 4 na Hakbang

Paggamit ng isang RTA Program Bilang isang Oscilloscope o Circuit Analyzer: Ang layunin ng trick na ito ay upang bigyan ang mga manonood at abot-kayang pagpipilian upang matingnan ang mga de-koryenteng signal ng kanilang mga circuit at aparato gamit ang mga programa ng real time analyzer (RTA). Ang pangunahing pakinabang sa pamamaraang ito sa isang oscilloscope ay ang mga programa sa RTA
