Paano Lumikha ng isang Temcor-style Geodesic Dome sa Autodesk Inventor: 8 Hakbang

2024 May -akda: John Day | [email protected]. Huling binago: 2024-01-30 13:14

Ipapakita sa iyo ng tutorial na ito kung paano lumikha ng isang temcor na istilo ng Temcor gamit lamang ang kaunting matematika.

Karamihan sa impormasyon sa tutorial na ito ay nakuha mula sa reverse-engineering ng TaffGoch ng pamamaraan ng subdivision ng lumang Amundsen-Scott South Pole Station, kaya isang malaking salamat sa kanya!

Ang isang pangunahing bentahe ng Temcor domes ay ang kanilang mababang natatanging strut count - tataas ito ng aritmetiko sa dalas, hindi katulad ng regular na triacontahedral geodesic grid ng Duncan Stuart (Paraan 3 *), ngunit ang resulta ay mukhang mas kaaya-aya.

Para sa pagiging simple, ang dalas ng simboryo na ginagawa namin ay 14, kaya't ang mga kadahilanan ng kuwerdas ay maaaring i-cross-check laban sa modelo ng Temcor ng TaffGoch.

Ang Inventor 2016.ipt ay kasama sa pagtatapos ng tutorial.

* I-UPDATE *

Inilarawan ko ang Paraan 4 bilang regular na triacontahedral geodesic grid ng Duncan Stuart, ngunit hindi. Ang pamamaraan ay talagang naimbento ni Christopher Kitrick, na, sa kanyang papel noong 1985, "Geodesic Domes", inilarawan ang pagtatayo nito. Bilang karagdagan, sa kanyang papel noong 1990, "Isang Pinag-isang Diskarte sa Class I, II & III Geodesic Domes", binabalangkas niya ang 8 iba pang mga pamamaraan, ang isa sa mga ito ay ang Pamamaraan 3 ni Duncan Stuart, ang isa ay kanyang sariling "Paraan 4", at, nakakagulat sapat na, isang pamamaraang hindi nakakaalam sa Temcor's, na tinawag niyang "Paraan aa" (ipinapakita ng Hakbang 7 kung paano binago ni Temcor ang "Paraan aa"). Sa hinaharap na maituturo, ilalarawan ko ang pagbuo ng mga pamamaraan na nakabalangkas sa huling papel.

Hakbang 1: Mga Parameter ng User

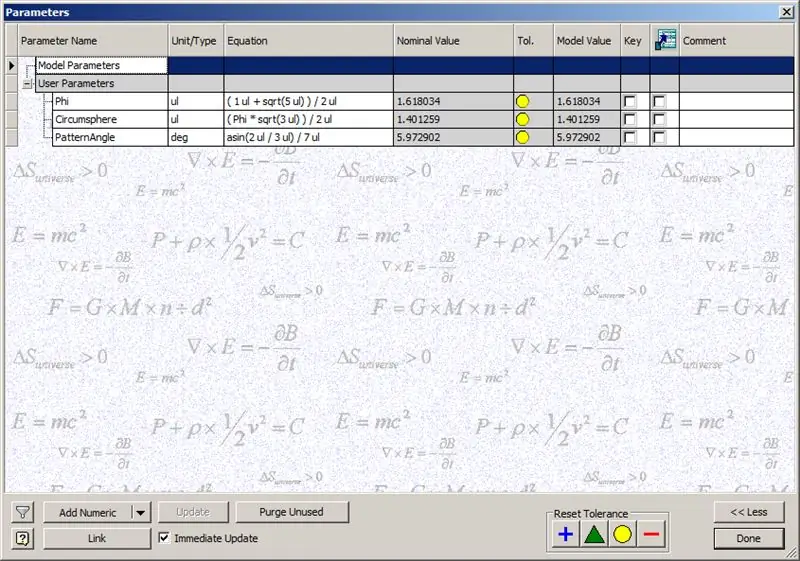
Bago kami magsimula sa pagbuo ng simboryo, ipasok ang mga parameter na ipinakita:

Phi - The Golden Ratio. Tinukoy bilang ((1 + √5 /) 2

Circumsphere - Ito ang circumsphere ng isang dodecahedron, na tinukoy bilang ((Phi * √3) / 2)

PatternAngle - Ito ang gitnang anggulo ng isang dodecahedron. Dahil ang dalas ng aming simboryo ay 14, hinati namin ang gitnang anggulo na ito sa kalahati ng dalas, sa kasong ito, 7.

Hakbang 2: Pag-sketch ng isang Golden Rectangle

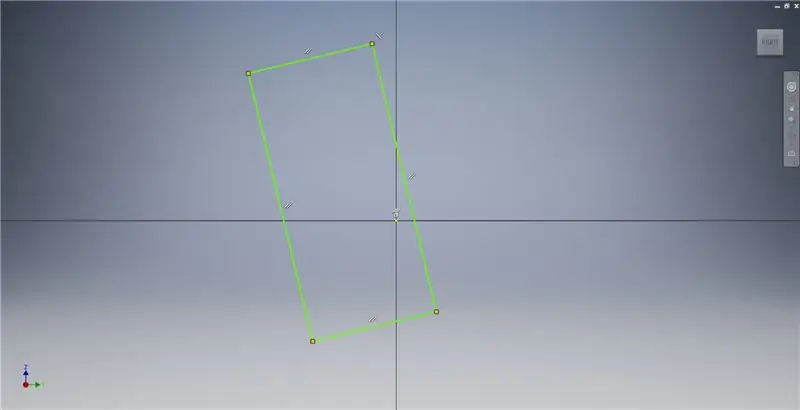
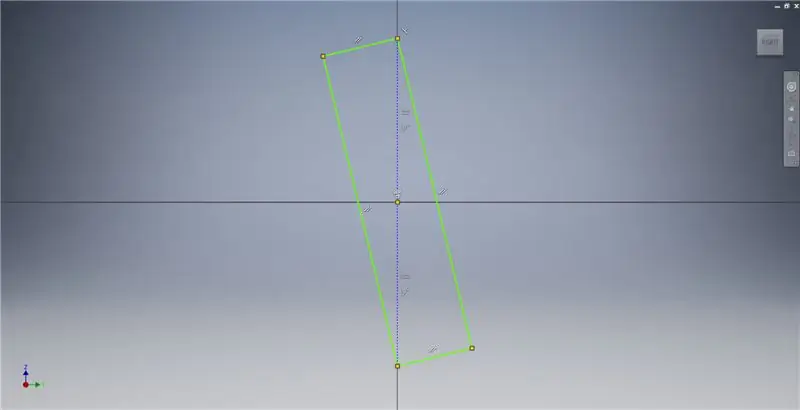
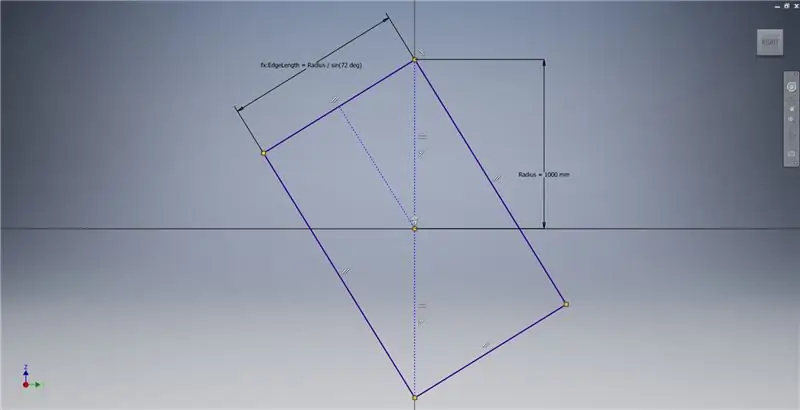
Magsimula ng isang sketch sa eroplano ng YZ, pagkatapos ay lumikha ng isang tatlong puntos na rektanggulo tulad ng ipinakita, na tumutukoy sa mga tala ng imahe para sa karagdagang impormasyon na naglalarawan sa paglikha ng isang Golden Rectangle.

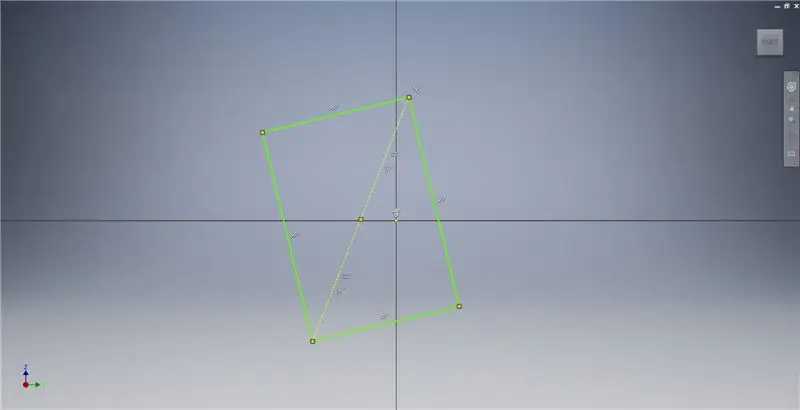
Hakbang 3: Lumilikha ng isang Golden² Rectangle

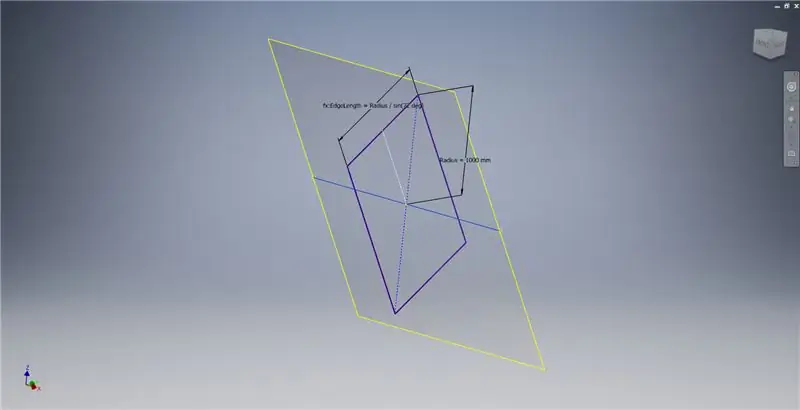
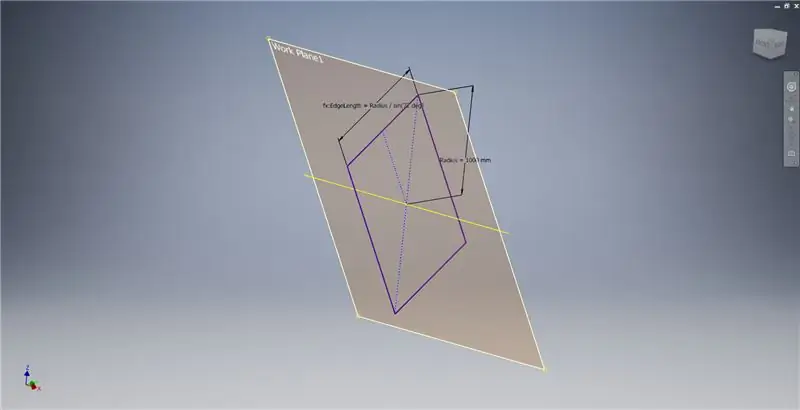
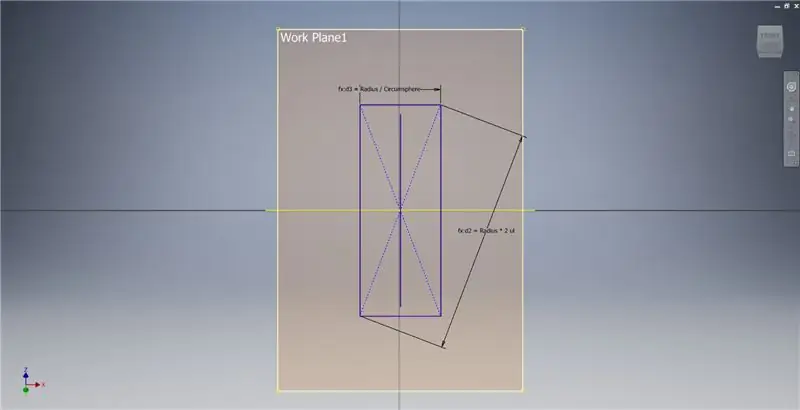
Lumikha ng isang eroplano sa trabaho gamit ang X axis at ang linya na naka-highlight sa unang imahe, pagkatapos ay magsimula ng isa pang sketch sa eroplano na ito. Bumuo ng isang centerpoint rektanggulo na nagsisimula mula sa pinagmulan, pagkatapos ay sukatin ang rektanggulo tulad ng ipinakita sa pangatlong imahe.

Hakbang 4: Lumilikha ng 2v Triacon Triangle

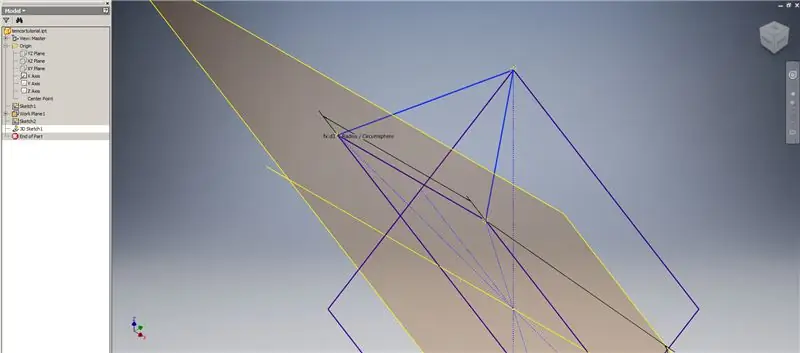
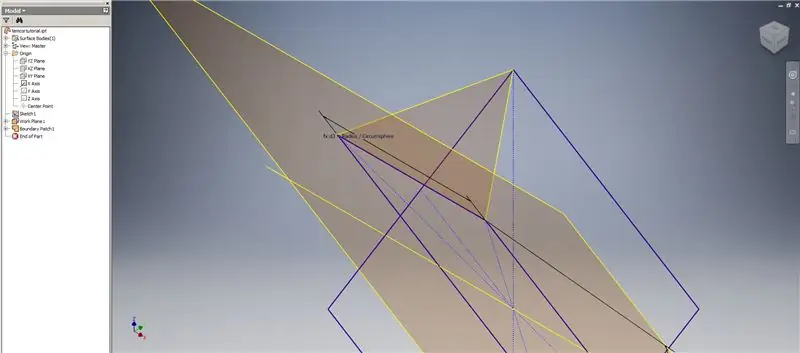
Ngayon na mayroon kaming lahat ng geometry na kailangan namin, buuin ang hangganan ng patch sa pangalawang imahe gamit ang anumang pamamaraan na gusto mo. Pinili kong gumawa ng 3D sketch, ngunit gagana rin ang pag-sketch sa isa pang eroplano.

Hakbang 5: Paglikha ng Mga Planong interseksyon

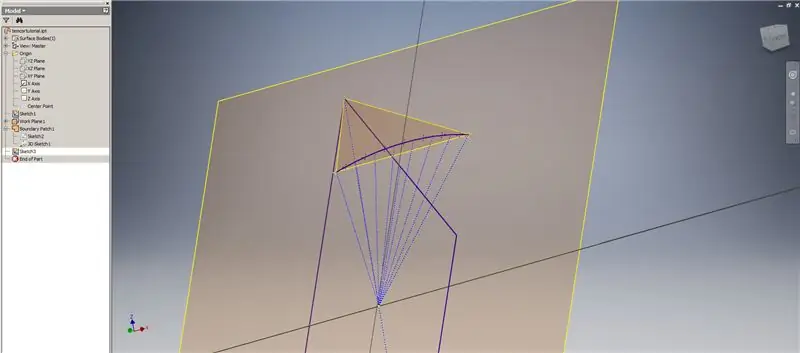
Magsimula ng isa pang sketch sa unang eroplano ng trabaho ("Plane ng Trabaho 1") na nilikha mo, i-project ang mga sulok ng Golden² Rectangle, pagkatapos ay ikonekta ang mga puntong ito at ang pinagmulan upang mabuo ang gitnang anggulo ng 2v triacontahedron. Hatiin ito sa kalahati ng dalas ng simboryo, na parang nagsisimula ka ng isang breakdown ng Paraan 2. Ilagay ang mga puntos sa mga midpoint ng chords.

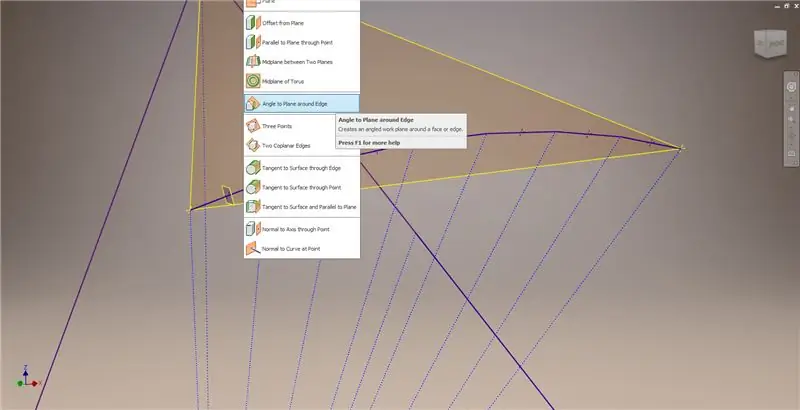
Lumabas sa sketch, pagkatapos ay lumikha ng isang eroplano gamit ang isa sa mga chords at ang midpoint nito, tulad ng ipinakita sa pangalawang imahe. Pagkatapos, lumikha ng isa pang eroplano sa trabaho gamit ang "Angle to Plane around Edge". Piliin ang Work Plane 1 at isa sa mga linya ng konstruksyon na ipinakita sa gitnang kanan at mas mababang kaliwang imahe. Tanggapin ang default na anggulo ng 90 degree, kung hindi man ang natitirang bahagi ng subdivision ay hindi magiging tama ang hitsura. Ulitin ang proseso gamit ang natitirang mga chords at mga linya ng konstruksyon upang makuha ang resulta sa ibabang kanang imahe.

Hakbang 6: Paglikha ng Mga Intersection Curve at Pagbubuo ng Subdivision

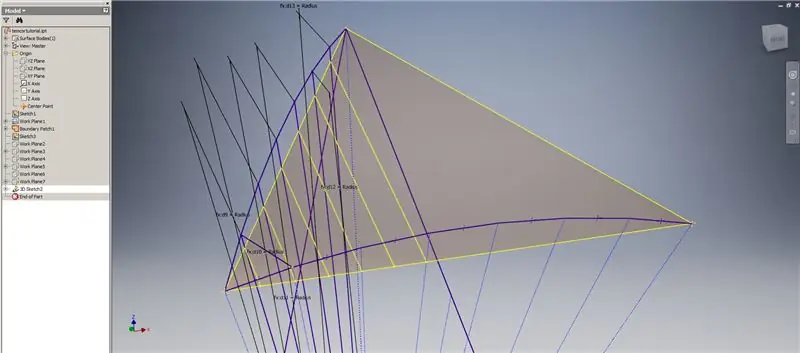
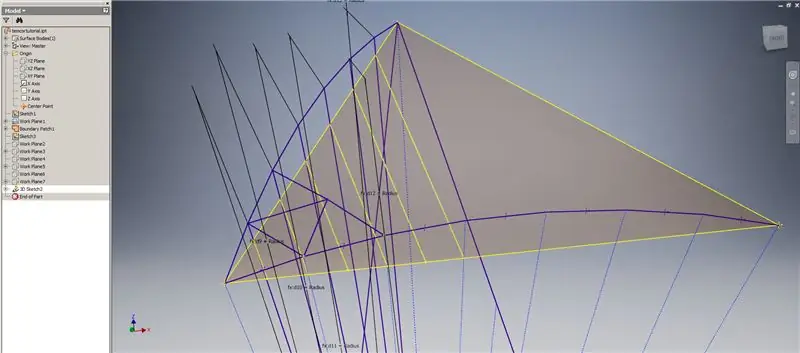
Magsimula ng isang 3D sketch, pagkatapos ay lumikha ng mga curve ng intersection gamit ang mga eroplano na gawa na iyong nilikha lamang at ang border patch, na bumubuo ng mga linya na ipinakita sa tuktok na imahe.

Gumuhit ng mga linya na magkakasabay sa mga endpoint ng mga kurba ng intersection tulad ng ipinakita sa Larawan 2. Gawin silang lahat katumbas ng radius ng simboryo. Iguhit ang mga kuwerdas na sumasali sa mga linya na namamalagi sa mga kurba ng intersection. Ikonekta ang anumang geometry na mukhang sapat na malapit upang makabuo ng isang tatsulok ng subdivision. Sumangguni sa susunod na 10 mga imahe kung saan ang mga chords ay mag-mirror sa mga eroplano sa interseksyon - maaari nila itong ipaliwanag nang mas mahusay kaysa sa mga salita lamang.

Hakbang 7: Pagkumpleto sa Dome

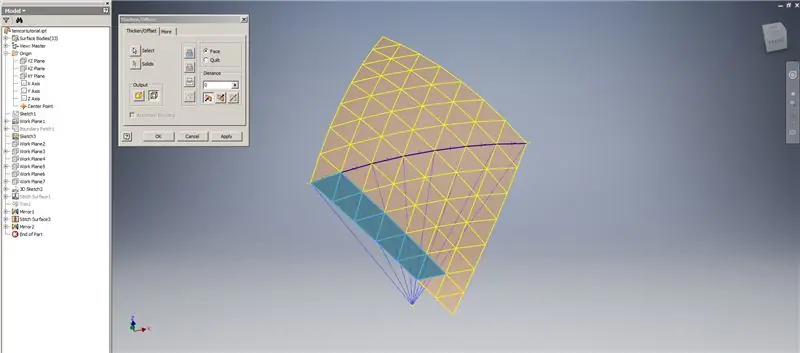
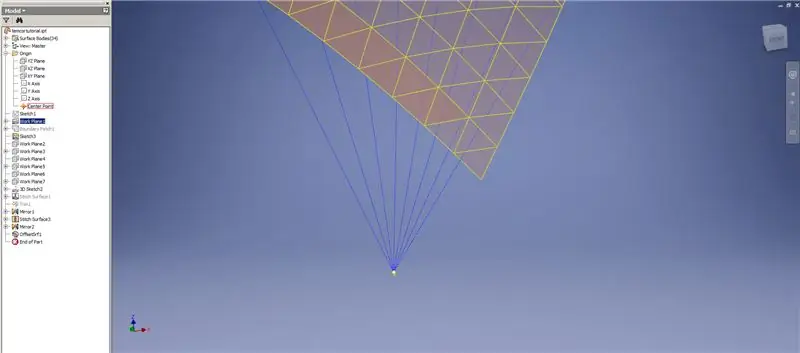
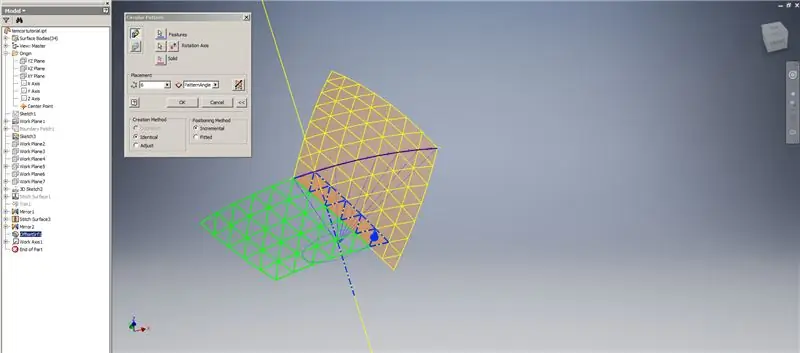
Lumikha ng isang Thued / Offset ng mga ilalim na hilera, tinatanggal ang huling dalawang hanay ng mga triangles. I-pattern ang bagong OffsetSrf 6 beses, o ((Frequency = 14) / 2) -1. Itago ang OffsetSrf, i-stitch ang mga pattern na ibabaw, pagkatapos ay i-mirror ang natahi na ibabaw sa YZ Plane. Lumikha ng mga eroplano sa trabaho na nakasalalay sa mga vertex ng tuktok na tatsulok, tulad ng ipinakita sa Larawan 6. Gupitin ang mga tahi at naka-mirror na mga ibabaw gamit ang mga bagong eroplano sa trabaho, pagkatapos ay tahiin ang natitirang mga ibabaw. I-pattern ang huling ibabaw na ito sa kabuuan ng Z axis, pagkatapos ay i-stitch ang mga huling ibabaw na ito nang magkasama, at tapos ka na!

Hakbang 8: Sinusuri ang Mga Chord

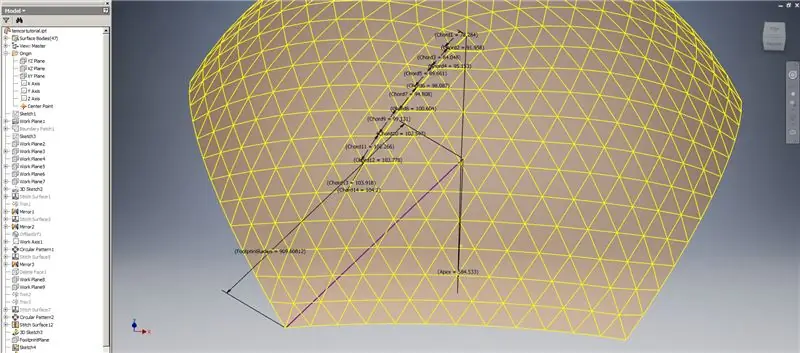
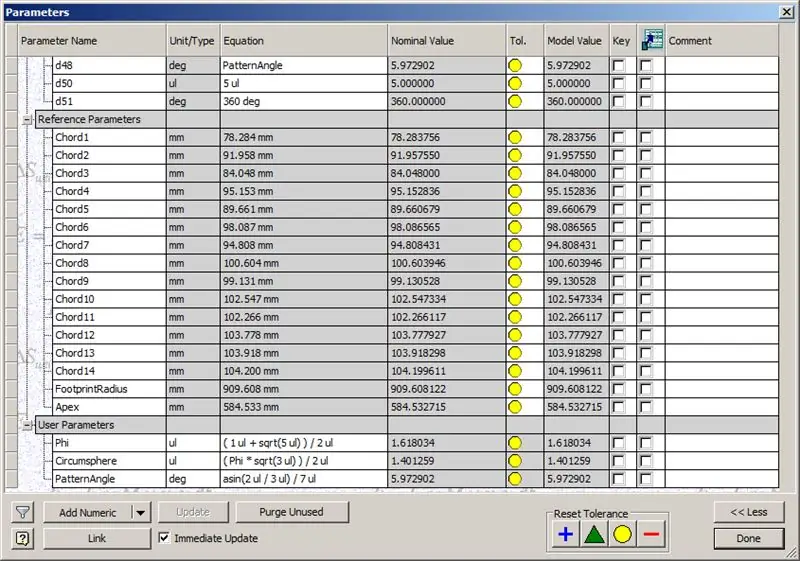
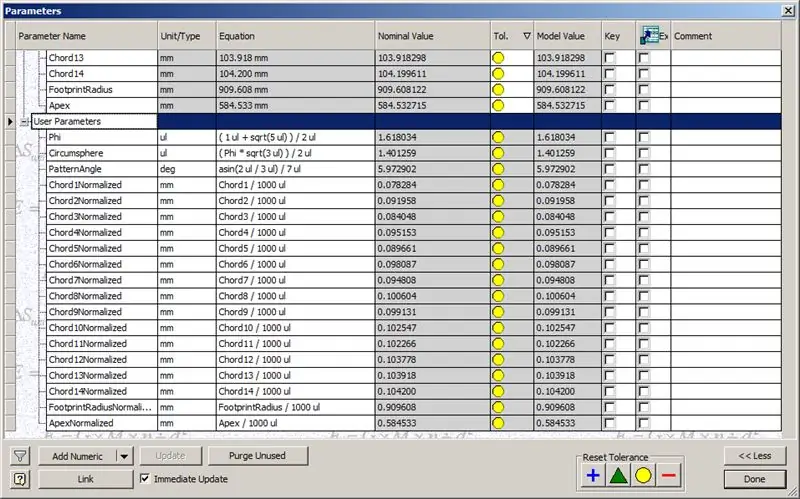
Kaya, natapos na ang aming simboryo, ngunit tingnan natin kung ang mga numero ay tumutugma sa modelo ni TaffGoch:

Pagpunta sa mga parameter ng sanggunian, mukhang perpekto ang mga ito!

Ang paghahati ng haba ng chord ng 1000, malinaw na nakikita namin ang isang perpektong pagsulat sa mga kadahilanan ng chord ng modelo ng TaffGoch, pati na rin ang footprint radius at mga apex factor.