
Talaan ng mga Nilalaman:
- Hakbang 1: Bumuo ng isang NxN Matrix ng Mga Unipormeng Kwadro
- Hakbang 2: Randomizing the Network
- Hakbang 3: Kumuha ng Mga Bagong Distansya
- Hakbang 4: Pumili ng isang Punto at Ihambing ang Distansya Mula sa Puntong Iyon sa Iba pa
- Hakbang 5: Lumipat sa isang Bagong Point
- Hakbang 6: Pilitin = K * distansya
- Hakbang 7: Baguhin ang Kilusan ng Network Dahil sa Moved Point
- Hakbang 8: Tapos na Code
- May -akda John Day day@howwhatproduce.com.
- Public 2024-01-30 13:14.
- Huling binago 2025-01-23 15:13.

Ang mga cell ay maaaring makipag-ugnay sa kanilang nakapaligid na extracellular matrix (ECM) at maaaring parehong mailapat pati na rin tumugon sa mga puwersang ipinataw ng ECM. Para sa aming proyekto, ginagaya namin ang isang magkakaugnay na network ng mga hibla na kikilos bilang ECM at makita kung paano nagbabago ang network bilang tugon sa paggalaw ng isa sa mga puntos. Ang ECM ay na-modelo bilang isang magkakaugnay na sistema ng mga bukal na una ay nasa balanse na may isang puwersang zero na zero. Tulad ng puwersa na inilalapat sa network bilang tugon sa paggalaw ng punto, sinubukan naming makuha ang mga nakakonektang puntos upang tumugon sa puwersa sa paraang tinangka nilang bumalik sa balanse. Ang puwersa ay sinusubaybayan ng equation F = k * x kung saan k ang spring spring at x ang pagbabago sa haba ng hibla. Ang simulation na ito ay makakatulong na magbigay ng isang pangkalahatang pag-unawa sa pagpapakalat ng puwersa sa mga fibrous network na maaaring magamit sa paglaon upang tulungan na gayahin ang mekanotransduction.
Hakbang 1: Bumuo ng isang NxN Matrix ng Mga Unipormeng Kwadro


Upang simulan ang code, pipiliin namin ang N na tutukoy sa mga sukat ng aming network (NxN). Ang halaga ng N ay maaaring manu-manong mabago upang mabago ang mga sukat ng network kung kinakailangan. Sa halimbawang ito, N = 8 kaya mayroon kaming isang 8x8 network ng mga puntos. Matapos naming mabuo ang matrix, ikonekta namin ang lahat ng mga puntos sa matrix na may haba ng 1 yunit gamit ang formula ng distansya, distansya = sqrt ((x2-x1) ^ 2 + (y2-y1) ^ 2). Sa pamamagitan nito, nakakakuha kami ng mga network ng mga parisukat na lahat ay pantay na spaced out ng 1 unit. Makikita ito sa figure 101.
Hakbang 2: Randomizing the Network


Sa hakbang na ito, nais naming i-randomize ang lahat ng mga lokasyon ng point maliban sa mga panlabas na puntos na bubuo sa aming hangganan. Upang magawa ito, nakita muna namin ang lahat ng mga coordinate ng matrix na katumbas ng 0 o N. Ang mga puntong ito ay ang mga bumubuo sa hangganan. Para sa mga di-hangganan na puntos, ang lokasyon ay na-randomize sa pamamagitan ng pagdaragdag ng isang iba't ibang mga random na halaga mula -.5 hanggang.5 sa parehong mga posisyon ng x at y. Ang naka-plot na randomized na imahe ay makikita sa Larawan 1.
Hakbang 3: Kumuha ng Mga Bagong Distansya

Kapag nagawa ang aming randomized network, mahahanap namin ang distansya sa pagitan ng mga konektadong puntos gamit ang formula ng distansya muli.
Hakbang 4: Pumili ng isang Punto at Ihambing ang Distansya Mula sa Puntong Iyon sa Iba pa



Sa hakbang na ito, maaari kaming pumili ng isang punto ng interes na ginagamit ang cursor, tulad ng ipinakita sa Larawan 2. Hindi mo kailangang ilipat ang iyong cursor nang eksakto sa puntong ito dahil isasaayos ito ng code sa pinakamalapit na koneksyon point. Upang magawa ito, kinakalkula muna namin ang distansya sa pagitan ng lahat ng mga konektadong puntos at ang puntong napili lamang namin. Matapos makalkula ang lahat ng mga distansya, pipiliin namin ang punto na may pinakamaliit na distansya mula sa napiling punto upang maging aktwal na napiling punto.
Hakbang 5: Lumipat sa isang Bagong Point



Sa hakbang na ito, gamit ang puntong napili sa nakaraang hakbang, inililipat namin ang punto sa isang bagong lokasyon. Ang kilusang ito ay ginagawa sa pamamagitan ng pagpili ng isang bagong posisyon gamit ang cursor na papalit sa dating posisyon. Ang kilusang ito ay gagamitin upang gayahin ang isang bigay na puwersa dahil sa pagbabago sa haba ng tagsibol. Sa lahat ng asul na pigura, isang bagong lokasyon ang napili. Sa susunod na pigura, ang paggalaw ay maaaring mailarawan ng mga koneksyon na kulay kahel na kung saan ay ang mga bagong lokasyon na taliwas sa mga asul na koneksyon na kung saan ay ang mga lumang lokasyon.
Hakbang 6: Pilitin = K * distansya

Sa hakbang na ito inilalapat namin ang puwersa ng equation = k * distansya, kung saan ang k ay isang pare-pareho 10 para sa mga fibre ng collagen. Dahil ang network ng hibla ay nagsisimula sa estado ng balanse nito, ang lakas na net ay 0. Lumilikha kami ng isang zero vector ang haba ng matrix na nabuo namin mas maaga upang kumatawan sa balanse na ito.
Hakbang 7: Baguhin ang Kilusan ng Network Dahil sa Moved Point




Sa hakbang na ito, ginaya namin ang paggalaw ng network bilang tugon sa paggalaw ng point upang bumalik sa estado ng balanse nito. Nagsisimula kami sa pamamagitan ng paghahanap ng mga bagong distansya sa pagitan ng dalawang puntos. Sa pamamagitan nito mahahanap natin ang pagbabago sa haba ng hibla sa pamamagitan ng pagtingin sa pagkakaiba sa pagitan ng luma at mga bagong distansya. Maaari din nating makita kung aling mga puntos ang lumipat at pati na rin ang mga puntos na konektado sa kanila sa pamamagitan ng paghahambing ng mga bago at lumang lokasyon ng point. Pinapayagan kaming makita kung aling mga puntong dapat lumipat bilang tugon sa lakas na pinaghirapan. Ang direksyon ng paggalaw ay maaaring masira sa mga x at y na bahagi nito, na nagbibigay ng isang vector ng direksyon ng 2D. Gamit ang k halaga, pagbabago sa distansya, at direksyon ng vector, maaari nating kalkulahin ang force vector na maaaring magamit upang ilipat ang aming mga puntos patungo sa balanse. Pinapatakbo namin ang seksyong ito ng code ng 100 beses, sa bawat oras na lumilipat sa mga pagtaas ng Force *.1. Ang pagpapatakbo ng code ng 100 beses ay nagbibigay-daan sa amin upang maabot muli ang balanse at sa pamamagitan ng pagpapanatili ng mga kundisyon ng hangganan nakikita namin ang isang pagbabago sa network sa halip na isang buong shift lamang. Ang paggalaw ng network ay makikita sa Larawan 3 na ang dilaw ay ang mga inilipat na posisyon at ang asul ay ang nauna.
Hakbang 8: Tapos na Code
Nakalakip sa seksyon na ito ay isang kopya ng aming code. Huwag mag-atubiling baguhin ito upang umangkop sa iyong mga pangangailangan sa pagmomodelo ng iba't ibang mga network!
Inirerekumendang:
Awtomatikong Magsimula ng isang Programa Kapag Nag-hook ng isang Laptop Sa isang Docking Station: 5 Mga Hakbang
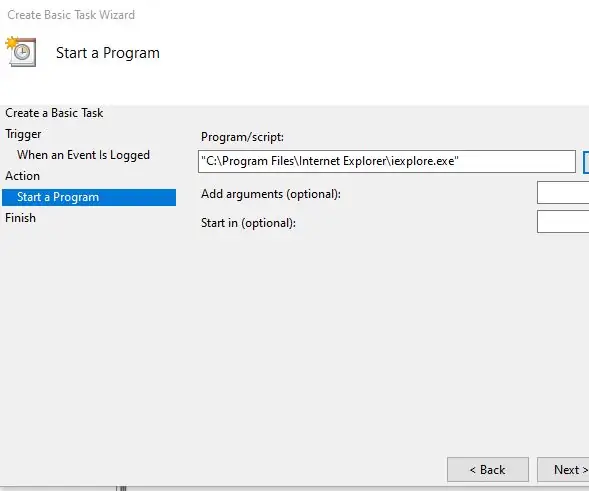
Awtomatikong Magsimula ng isang Programa Kapag Ang Pag-hook ng isang Laptop Sa isang Docking Station: Ang itinuturo na ito ay tungkol sa kung paano magpatakbo ng isang programa o isang application kapag na-hook mo ang iyong laptop sa isang docking station. Sa halimbawang ito gumagamit ako ng Lenovo T480 Windows 10
Pagkuha ng Pagbabago ng Temperatura Mula sa Pagbabago ng Klima sa Python: 6 Mga Hakbang
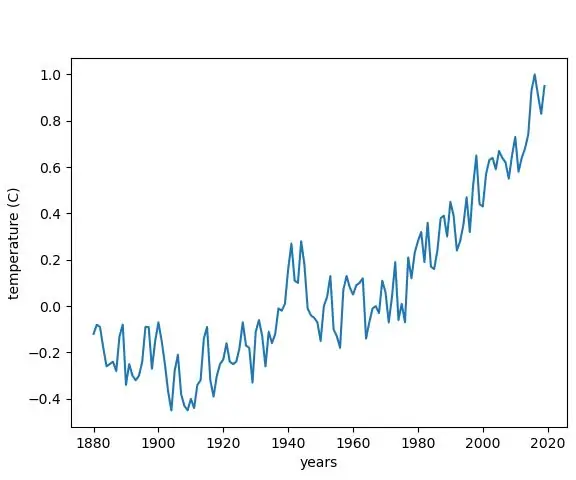
Pagkuha ng Pagbabago ng Temperatura Mula sa Pagbabago ng Klima sa Python: Ang Pagbabago ng Klima ay isang malaking problema. At maraming tao ang hindi ngayon kung gaano ito nabuhay. Sa itinuturo na ito, isasalamin namin ang pagbabago ng temperatura sa klima dahil sa pagbabago ng klima. Para sa isang cheat sheet, maaari mong tingnan ang python file sa ibaba
Mga Binuong Surfboard ng Data: 11 Mga Hakbang (na may Mga Larawan)

Mga Binuong Data na Surfboard: Kinuha ito mula sa aking nakatatandang thesis sa Industrial Design mula noong isang taon na ang nakalilipas kaya paumanhin kung may ilang mga butas dito maaaring hindi masyadong naalala ang aking memorya. Ito ay isang pang-eksperimentong proyekto at maraming mga bagay na maaaring nagawa nang iba, don
Gumawa ng isang Panlabas na HDD Mula sa Lumang Panlabas na CD / RW: 5 Hakbang

Gumawa ng isang Panlabas na HDD Mula sa Lumang Panlabas na CD / RW: Medyo tuwid na pasulong na pag-convert ng isang lumang panlabas na cd / rw sa isang mas kapaki-pakinabang na panlabas na hard drive. Mga supplies1-panlabas na cd / rw (mas mabuti ang mas boxy type) 1-hard drive (dapat na tumugma sa panloob na konektor ng drive case, kailangang mai-format / sysed) 1-sm
Paano Baguhin ang Tekstong Lilitaw Kapag Inilipat Mo ang Iyong Mouse sa Simula ng Button: 4 Mga Hakbang
Paano Baguhin ang Tekstong Lilitaw Kapag Inilipat Mo ang Iyong Mouse sa Simula ng Simula: Sinasabi sa pamagat ang lahat
