
Talaan ng mga Nilalaman:
- May -akda John Day day@howwhatproduce.com.
- Public 2024-01-30 13:16.
- Huling binago 2025-01-23 15:13.
Panimula
Ang gabay na ito ay inilaan sa lahat na interesado sa paggamit ng mga Accelerometers at Gyroscope pati na rin ang mga kombinasyon ng mga aparato ng IMU (Inertial Measurement Unit) sa kanilang mga proyekto sa electronics
Tatakpan namin:
- Ano ang sinusukat ng isang accelerometer?
- Ano ang sinusukat ng isang gyroscope (aka gyro)?
- Paano i-convert ang mga pagbabasa ng analog-to-digital (ADC) na nakukuha mo mula sa mga sensor na ito sa mga pisikal na yunit (iyon ay magiging g para sa accelerometer, deg / s para sa gyroscope)
- Paano pagsamahin ang mga pagbasa ng accelerometer at gyroscope upang makakuha ng tumpak na impormasyon tungkol sa pagkahilig ng iyong aparato na may kaugnayan sa ground plane
Sa buong artikulo susubukan kong panatilihing minimum ang matematika. Kung alam mo kung ano ang Sine / Cosine / Tangent pagkatapos ay dapat mong maunawaan at magamit ang mga ideyang ito sa iyong proyekto kahit na anong platform ang ginagamit mo: Arduino, Propeller, Basic Stamp, Atmel chips, Microchip PIC, atbp.
Mayroong mga tao roon na naniniwala na kailangan mo ng kumplikadong matematika upang magamit ang isang yunit ng IMU (kumplikadong mga filter ng FIR o IIR tulad ng mga filter ng Kalman, mga filter ng Parks-McClellan, atbp.). Maaari kang magsaliksik ng lahat ng mga iyon at makamit ang kahanga-hanga ngunit kumplikadong mga resulta. Ang aking paraan ng pagpapaliwanag ng mga bagay ay nangangailangan lamang ng pangunahing matematika. Ako ay isang dakilang naniniwala sa pagiging simple. Sa palagay ko ang isang system na simple ay mas madaling kontrolin at subaybayan, bukod sa maraming mga naka-embed na aparato ay walang kapangyarihan at mga mapagkukunan upang magpatupad ng mga kumplikadong algorithm na nangangailangan ng mga kalkulasyon ng matrix.
Gagamitin ko bilang isang halimbawa ng isang bagong yunit ng IMU, ang Acc_Gyro Accelerometer + Gyro IMU. Gagamitin namin ang mga parameter ng aparatong ito sa aming mga halimbawa sa ibaba. Ang yunit na ito ay isang mahusay na aparato upang magsimula dahil binubuo ito ng 2 mga aparato:
- LIS331AL (sheet ng data) - isang triaxial 2G accelerometer - LPR550AL (sheet ng data) - isang dalawahang-axis pitch at roll, 500 deg / sec gyroscope
Sama-sama nilang kinakatawan ang isang 5-Degree ng Freedom Inertial Measurement Unit. Ngayon ay isang magarbong pangalan! Gayunpaman, sa likod ng magarbong pangalan ay isang napaka kapaki-pakinabang na aparato ng kumbinasyon na sasakupin namin at ipaliwanag namin nang detalyado sa gabay na ito.
Hakbang 1: Ang Accelerometer
Upang maunawaan ang yunit na ito magsisimula tayo sa accelerometer. Kapag nag-iisip tungkol sa mga accelerometro madalas na kapaki-pakinabang upang mag-imahe ng isang kahon sa hugis ng isang kubo na may isang bola sa loob nito. Maaari mong isipin ang iba pa tulad ng isang cookie o isang donut, ngunit mag-iisip ako ng isang bola:
Kung dadalhin namin ang kahon na ito sa isang lugar na walang mga gravitation field o para sa bagay na iyon na walang iba pang mga patlang na maaaring makaapekto sa posisyon ng bola - ang bola ay lumulutang lamang sa gitna ng kahon. Maaari mong isipin na ang kahon ay nasa kalawakan na kalayuan na malayo sa anumang mga pang-cosmic na katawan, o kung ang nasabing lugar ay mahirap hanapin isipin kahit papaano ang isang space craft na umiikot sa paligid ng planeta kung saan ang lahat ay nasa walang timbang na estado. Mula sa larawan sa itaas maaari mong makita na nagtatalaga kami sa bawat axis ng isang pares ng mga pader (inalis namin ang pader Y + upang tumingin kami sa loob ng kahon). Isipin na ang bawat pader ay sensitibo sa presyon. Kung ilipat natin bigla ang kahon sa kaliwa (binibilis natin ito sa bilis ng 1g = 9.8m / s ^ 2), ang bola ay tatama sa pader X-. Sinusukat namin ang puwersang presyon na nalalapat ang bola sa dingding at naglalabas ng halagang -1g sa X axis.
Mangyaring tandaan na ang accelerometer ay talagang makakakita ng isang puwersa na nakadirekta sa kabaligtaran na direksyon mula sa acceleration vector. Ang puwersang ito ay madalas na tinatawag na Inertial Force o Fictitious Force. Ang isang bagay na dapat mong malaman mula dito ay ang isang accelerometer na sumusukat sa pagpabilis nang hindi direkta sa pamamagitan ng isang puwersa na inilalapat sa isa sa mga pader nito (ayon sa aming modelo, maaaring ito ay isang tagsibol o iba pa sa mga tunay na accelerator ng buhay). Ang puwersang ito ay maaaring sanhi ng pagbilis, ngunit tulad ng makikita natin sa susunod na halimbawa hindi ito palaging sanhi ng pagbilis.
Kung kukunin namin ang aming modelo at ilagay ito sa Earth ang bola ay mahuhulog sa Z-wall at maglalapat ng lakas na 1g sa ibabang pader, tulad ng ipinakita sa larawan sa ibaba:
Sa kasong ito ang kahon ay hindi gumagalaw ngunit nakakakuha pa rin kami ng pagbabasa ng -1g sa Z axis. Ang presyon na inilapat ng bola sa dingding ay sanhi ng isang puwersang gravitation. Sa teorya maaaring ito ay isang iba't ibang uri ng puwersa - halimbawa, kung akala mo na ang aming bola ay metal, ang paglalagay ng isang magnet sa tabi ng kahon ay maaaring ilipat ang bola kaya't tumama ito sa ibang pader. Ito ay sinabi lamang upang patunayan na sa kakanyahan ang mga hakbang sa bilis ng sukat ng puwersa ay hindi pinabilis. Nangyayari lamang na ang pagpabilis ay nagdudulot ng isang puwersang inertial na nakuha ng mekanismo ng puwersa ng pagkakita ng accelerometer.
Habang ang modelong ito ay hindi eksakto kung paano itinayo ang isang sensor ng MEMS madalas itong kapaki-pakinabang sa paglutas ng mga problema na nauugnay sa accelerometer. Mayroong talagang mga katulad na sensor na mayroong mga metal na bola sa loob, tinatawag silang mga ikiling na switch, subalit mas primitive sila at karaniwang masasabi lamang nila kung ang aparato ay may hilig sa loob ng ilang saklaw o hindi, hindi sa lawak ng pagkahilig.
Sa ngayon sinuri namin ang output ng accelerometer sa isang solong axis at ito lang ang makukuha mo sa isang solong axometropometter. Ang totoong halaga ng mga triaxial accelerometers ay nagmula sa katotohanang maaari silang makakita ng mga puwersang hindi gumagalaw sa lahat ng tatlong palakol. Bumalik tayo sa aming modelo ng kahon, at paikutin natin ang kahon ng 45 degree sa kanan. Hahawakan ng bola ang 2 pader ngayon: Z- at X- tulad ng ipinakita sa larawan sa ibaba:
Ang mga halagang 0.71 ay hindi arbitraryo, ang mga ito ay talagang isang pagtatantya para sa SQRT (1/2). Ito ay magiging mas malinaw sa aming pagpapakilala sa aming susunod na modelo para sa accelerometer.
Sa nakaraang modelo ay naayos namin ang puwersa ng gravitation at pinaikot ang aming haka-haka na kahon. Sa huling 2 mga halimbawa nasuri namin ang output sa 2 magkakaibang mga posisyon sa kahon, habang ang force vector ay nanatiling pare-pareho. Bagaman kapaki-pakinabang ito sa pag-unawa sa kung paano nakikipag-ugnay ang accelerometer sa mga puwersa sa labas, mas praktikal na magsagawa ng mga kalkulasyon kung aayusin namin ang coordinate system sa mga palakol ng accelerometer at isipin na ang force vector ay umiikot sa paligid natin.
Mangyaring tingnan ang modelo sa itaas, napanatili ko ang mga kulay ng mga palakol upang makagawa ka ng isang mental na paglipat mula sa nakaraang modelo hanggang sa bago. Isipin lamang na ang bawat axis sa bagong modelo ay patayo sa kani-kanilang mga mukha ng kahon sa nakaraang modelo. Ang vector R ay ang force vector na sinusukat ng accelerometer (maaari itong alinman sa puwersa ng gravitation o ang puwersang hindi gumagalaw mula sa mga halimbawa sa itaas o isang kombinasyon ng pareho). Ang Rx, Ry, Rz ay projection ng R vector sa X, Y, Z axes. Mangyaring pansinin ang sumusunod na ugnayan:
R ^ 2 = Rx ^ 2 + Ry ^ 2 + Rz ^ 2 (Eq. 1)
na karaniwang katumbas ng Pythagorean theorem sa 3D.
Tandaan na kaunti kanina sinabi ko sa iyo na ang mga halaga ng SQRT (1/2) ~ 0.71 ay hindi sapalaran. Kung i-plug mo ang mga ito sa formula sa itaas, pagkatapos na alalahanin na ang aming puwersa ng gravitation ay 1 g maaari naming mapatunayan na:
1 ^ 2 = (-SQRT (1/2)) ^ 2 + 0 ^ 2 + (-SQRT (1/2)) ^ 2
sa pamamagitan lamang ng pagpapalit ng R = 1, Rx = -SQRT (1/2), Ry = 0, Rz = -SQRT (1/2) sa Eq.1
Matapos ang isang mahabang paunang salita ng teorya papalapit kami sa mga accelerometers ng totoong buhay. Ang mga halagang Rx, Ry, Rz ay talagang linear na nauugnay sa mga halagang maia-output ng iyong real-life accelerometer at maaari mong gamitin para sa pagganap ng iba't ibang mga kalkulasyon.
Bago kami makarating doon pag-usapan natin nang kaunti tungkol sa kung paano ihahatid sa amin ng mga accelerometers ang impormasyong ito. Karamihan sa mga accelerometro ay mahuhulog sa dalawang kategorya: digital at analog. Magbibigay sa iyo ang mga digital accelerometers ng impormasyon gamit ang isang serial protocol tulad ng I2C, SPI o USART, habang ang mga analog accelerometers ay maglalabas ng antas ng boltahe sa loob ng isang paunang natukoy na saklaw na kailangan mong i-convert sa isang digital na halaga gamit ang isang ADC (analog sa digital converter) na module. Hindi ko bibigyan ang detalye tungkol sa kung paano gumagana ang ADC, bahagyang dahil ito ay isang malawak na paksa at bahagyang dahil iba ito mula sa isang platform patungo sa isa pa. Ang ilang mga microcontroller ay magkakaroon ng built-in na mga module ng ADC na ang ilan sa mga ito ay mangangailangan ng mga panlabas na sangkap upang maisagawa ang mga conversion sa ADC. Hindi alintana kung anong uri ng module ng ADC na ginagamit mo magtatapos ka sa isang halaga sa isang tiyak na saklaw. Halimbawa ang isang 10-bit na module ng ADC ay maglalabas ng isang halaga sa saklaw ng 0..1023, tandaan na 1023 = 2 ^ 10 -1. Ang isang 12-bit na ADC module ay maglalabas ng isang halaga sa saklaw ng 0..4095, tandaan na 4095 = 2 ^ 12-1.
Magpatuloy tayo sa pamamagitan ng pagsasaalang-alang ng isang simpleng halimbawa, ipagpalagay na binigyan kami ng aming module ng 10bit ADC ng mga sumusunod na halaga para sa tatlong mga channel ng accelerometer (axes):
AdcRx = 586 AdcRy = 630 AdcRz = 561
Ang bawat module ng ADC ay magkakaroon ng isang boltahe ng sanggunian, ipagpalagay natin sa aming halimbawa na ito ay 3.3V. Upang mai-convert ang isang 10bit na halaga ng adc sa boltahe ginagamit namin ang sumusunod na formula:
VoltsRx = AdcRx * Vref / 1023
Isang mabilis na tala dito: na para sa 8bit ADC ang huling divider ay magiging 255 = 2 ^ 8 -1, at para sa 12bit ADC na huling divider ay magiging 4095 = 2 ^ 12 -1.
Ang paglalapat ng formula na ito sa lahat ng 3 mga channel na nakukuha namin:
VoltsRx = 586 * 3.3V / 1023 = ~ 1.89V (ikot namin ang lahat ng mga resulta sa 2 decimal point) VoltsRy = 630 * 3.3V / 1023 = ~ 2.03V VoltsRz = 561 * 3.3V / 1023 = ~ 1.81V
Ang bawat accelerometer ay may antas na zero-g boltahe, mahahanap mo ito sa mga detalye, ito ang boltahe na tumutugma sa 0g. Upang makakuha ng isang naka-sign na halaga ng boltahe kailangan naming kalkulahin ang shift mula sa antas na ito. Sabihin nating ang aming 0g antas ng boltahe ay VzeroG = 1.65V. Kinakalkula namin ang boltahe na nagbabago mula sa zero-g boltahe tulad ng sumusunod:
DeltaVoltsRx = 1.89V - 1.65V = 0.24V DeltaVoltsRy = 2.03V - 1.65V = 0.38V DeltaVoltsRz = 1.81V - 1.65V = 0.16V
Mayroon na kaming mga pagbabasa ng accelerometer sa Volts, wala pa rin sa g (9.8 m / s ^ 2), upang gawin ang pangwakas na conversion na inilalapat namin ang pagkasensitibo ng accelerometer, na karaniwang ipinahiwatig sa mV / g. Hinahayaan nating sabihin ang aming Sensitivity = 478.5mV / g = 0.4785V / g. Ang mga halaga ng pagkasensitibo ay matatagpuan sa mga pagtutukoy ng accelerometer. Upang makuha ang panghuling halaga ng lakas na ipinahiwatig sa g ginagamit namin ang sumusunod na pormula:
Rx = DeltaVoltsRx / Sensitivity
Rx = 0.24V / 0.4785V / g = ~ 0.5g Ry = 0.38V / 0.4785V / g = ~ 0.79g Rz = 0.16V / 0.4785V / g = ~ 0.33g
Maaari naming syempre pagsamahin ang lahat ng mga hakbang sa isang pormula, ngunit dumaan ako sa lahat ng mga hakbang upang linawin kung paano ka mula sa mga pagbabasa ng ADC patungo sa isang sangkap ng force vector na ipinahiwatig sa g.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Sensitivity (Eq.2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Sensitivity Rz = (AdcRz * Vref / 1023 - VzeroG) / Sensitivity
Mayroon kaming lahat ng 3 mga bahagi na tumutukoy sa aming inertial force vector, kung ang aparato ay hindi napapailalim sa iba pang mga puwersa maliban sa gravitation, maaari nating ipalagay na ito ang direksyon ng aming gravitation force vector. Kung nais mong kalkulahin ang pagkahilig ng aparato na may kaugnayan sa lupa maaari mong kalkulahin ang anggulo sa pagitan ng vector at Z axis na ito. Kung interesado ka rin sa direksyon ng pagkagusto ng bawat axis maaari mong hatiin ang resulta na ito sa 2 bahagi: pagkahilig sa X at Y axis na maaaring kalkulahin bilang angulo sa pagitan ng gravitation vector at X / Y axes. Ang pagkalkula ng mga anggulong ito ay mas simple kaysa sa maaari mong isipin, ngayong kinakalkula namin ang mga halaga para sa Rx, Ry at Rz. Bumalik tayo sa aming huling modelo ng accelerometer at gumawa ng ilang karagdagang mga notasyon:
Ang mga anggulo na interesado kami ay ang mga anggulo sa pagitan ng X, Y, Z axes at ang force vector R. Tatukoyin namin ang mga anggulong ito bilang Axr, Ayr, Azr. Maaari mong mapansin mula sa kanang sulok na tatsulok na nabuo ng R at Rx na:
cos (Axr) = Rx / R, at katulad nito: cos (Ayr) = Ry / R cos (Azr) = Rz / R
Maaari naming ibawas mula sa Eq.1 na R = SQRT (Rx ^ 2 + Ry ^ 2 + Rz ^ 2).
Mahahanap natin ngayon ang aming mga anggulo sa pamamagitan ng paggamit ng mga function ng arccos () (ang kabaligtaran na cos () na pag-andar):
Axr = arccos (Rx / R) Ayr = arccos (Ry / R) Azr = arccos (Rz / R)
Malayo na ang narating namin upang ipaliwanag ang modelo ng accelerometer, upang makabuo lamang ng mga formula na ito. Nakasalalay sa iyong mga aplikasyon baka gusto mong gumamit ng anumang mga intermediate na formula na nakuha namin. Ipapakilala din namin ang modelo ng gyroscope sa lalong madaling panahon, at makikita natin kung paano maaaring pagsamahin ang data ng accelerometer at gyroscope upang makapagbigay ng mas tumpak na mga pagtatantya ng pagkahilig.
Ngunit bago natin gawin iyon gumawa muna tayo ng mas maraming kapaki-pakinabang na mga notasyon:
cosX = cos (Axr) = Rx / R cozy = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
Ang triplet na ito ay madalas na tinatawag na Direction Cosine, at karaniwang kinakatawan nito ang unit vector (vector na may haba na 1) na may parehong direksyon sa aming R vector. Madali mong mapatunayan iyon:
SQRT (cosX ^ 2 + komportable ^ 2 + cosZ ^ 2) = 1
Ito ay isang magandang pag-aari dahil pinawalan tayo nito mula sa pagsubaybay sa modulus (haba) ng R vector. Kadalasan mga oras kung interesado lamang kami sa direksyon ng aming inertial vector, makatuwiran na gawing normal ang modulus upang gawing simple ang iba pang mga kalkulasyon.
Hakbang 2: Gyroscope
Hindi namin ipakikilala ang anumang katumbas na modelo ng kahon para sa gyroscope tulad ng ginawa namin para sa accelerometer, sa halip ay tumalon kami diretso sa pangalawang modelo ng accelerometer at ipapakita namin kung ano ang sinusukat ng gyroscope ayon sa modelong ito.
Sinusukat ng bawat channel ng gyroscope ang pag-ikot sa paligid ng isa sa mga palakol. Halimbawa ang isang 2-axes gyroscope ay susukat sa pag-ikot sa paligid (o maaaring sabihin ng ilan na "tungkol sa") ang mga axis ng X at Y. Upang maipahayag ang pag-ikot na ito sa mga numero gumawa tayo ng ilang mga notasyon. Tukuyin muna natin:
Ang Rxz - ay ang projection ng inertial force vector R sa eroplano na XZ na Ryz - ay ang projection ng inertial force vector R sa eroplano ng YZ
Mula sa kanang sulok na tatsulok na nabuo ni Rxz at Rz, gamit ang teorama ng Pythagorean na nakukuha namin:
Rxz ^ 2 = Rx ^ 2 + Rz ^ 2, at katulad nito: Ryz ^ 2 = Ry ^ 2 + Rz ^ 2
tandaan din na:
R ^ 2 = Rxz ^ 2 + Ry ^ 2, maaari itong makuha mula sa Eq.1 at mas mataas na mga equation, o maaari itong makuha mula sa kanang-anggulo na tatsulok na nabuo ng R at Ryz R ^ 2 = Ryz ^ 2 + Rx ^ 2
Hindi namin gagamitin ang mga formula na ito sa artikulong ito ngunit kapaki-pakinabang na tandaan ang ugnayan sa pagitan ng lahat ng mga halaga sa aming modelo.
Sa halip bibigyan namin ng kahulugan ang anggulo sa pagitan ng Z axis at Rxz, Ryz vector tulad ng sumusunod:
Ang Axz - ay ang anggulo sa pagitan ng Rxz (projection ng R sa XZ na eroplano) at Z axis na Ayz - ay ang anggulo sa pagitan ng Ryz (projection ng R sa YZ na eroplano) at Z axis
Ngayon ay papalapit na kami sa kung ano ang sinusukat ng gyroscope. Sinusukat ng Gyroscope ang rate ng mga pagbabago ng mga anggulong tinukoy sa itaas. Sa madaling salita ay maglalabas ito ng isang halaga na tuwirang nauugnay sa rate ng pagbabago ng mga anggulong ito. Upang ipaliwanag ito ay ipagpalagay natin na nasusukat natin ang anggulo ng pag-ikot sa paligid ng axis Y (iyon ang magiging anggulo ng Axz) sa oras na t0, at tinukoy namin ito bilang Axz0, susunod na sinukat namin ang anggulong ito sa ibang oras t1 at ito ay Axz1. Ang rate ng pagbabago ay makakalkula tulad ng sumusunod:
RateAxz = (Axz1 - Axz0) / (t1 - t0).
Kung ipahayag namin ang Axz sa mga degree, at oras sa mga segundo, pagkatapos ang halagang ito ay ipapakita sa deg / s. Ito ang sinusukat ng isang gyroscope.
Sa pagsasagawa ng isang gyroscope (maliban kung ito ay isang espesyal na digital gyroscope) ay bihirang magbigay sa iyo ng isang halagang ipinahayag sa deg / s. Kapareho ng para sa accelerometer makakakuha ka ng isang halaga ng ADC na kakailanganin mong i-convert sa deg / s gamit ang isang formula na katulad ng Eq. 2 na tinukoy namin para sa accelerometer. Ipakilala natin ang ADC sa deg / s conversion formula para sa gyroscope (ipinapalagay namin na gumagamit kami ng isang 10bit ADC module, para sa 8bit ADC palitan ang 1023 ng 255, para sa 12bit ADC palitan ang 1023 ng 4095).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sensitivity
Ang AdcGyroXZ, AdcGyroYZ - ay nakuha mula sa aming module ng adc at kinakatawan nila ang mga channel na sumusukat sa pag-ikot ng projection ng R vector sa XZ ayon sa pagkakabanggit sa mga YZ na eroplano, na katumbas ng pagsasabing ang pag-ikot ay ginawa sa paligid ng Y at X axes ayon sa pagkakabanggit.
Ang Vref - ay ang boltahe ng sanggunian ng ADC na gagamitin namin ng 3.3V sa halimbawa sa ibaba VzeroRate - ay ang boltahe na zero-rate, sa madaling salita ang boltahe na output ng gyroscope kapag hindi ito napapailalim sa anumang pag-ikot, para sa board ng Acc_Gyro ito ay halimbawa 1.23V (mahahanap mo ang mga halagang ito sa mga detalye) Sensitivity - ay ang pagiging sensitibo ng iyong gyroscope na ito ay ipinahayag sa mV / (deg / s) na madalas na nakasulat bilang mV / deg / s, karaniwang sasabihin nito sa iyo kung gaano karaming mV ang tumaas ang output ng gyroscope, kung taasan mo ang bilis ng pag-ikot ng isang deg / s. Ang pagiging sensitibo ng Acc_Gyro board ay halimbawa 2mV / deg / s o 0.002V / deg / s
Kumuha tayo ng isang halimbawa, ipagpalagay na ang aming module ng ADC ay nagbalik ng mga sumusunod na halaga:
AdcGyroXZ = 571 AdcGyroXZ = 323
Gamit ang formula sa itaas, at ang paggamit ng mga parameter ng detalye ng Acc_Gyro board makukuha namin:
RateAxz = (571 * 3.3V / 1023 - 1.23V) / (0.002V / deg / s) = ~ 306 deg / s RateAyz = (323 * 3.3V / 1023 - 1.23V) / (0.002V / deg / s) = ~ -94 deg / s
Sa madaling salita umiikot ang aparato sa axis ng Y (o masasabi nating umiikot ito sa XZ na eroplano) na may bilis na 306 deg / s at sa paligid ng X axis (o masasabi nating umiikot ito sa YZ na eroplano) na may bilis ng - 94 deg / s. Mangyaring tandaan na ang negatibong pag-sign ay nangangahulugan na ang aparato ay umiikot sa kabaligtaran na direksyon mula sa maginoo na positibong direksyon. Sa pamamagitan ng kombensiyon ang isang direksyon ng pag-ikot ay positibo. Ipapakita sa iyo ng isang mahusay na sheet ng pagtutukoy ng gyroscope kung aling direksyon ang positibo, kung hindi man makikita mo ito sa pamamagitan ng pag-eksperimento sa aparato at tandaan kung aling direksyon ng pag-ikot ang nagreresulta sa pagtaas ng boltahe sa output pin. Ito ay pinakamahusay na ginagawa gamit ang isang oscilloscope dahil sa lalong madaling itigil mo ang pag-ikot ang boltahe ay babagsak pabalik sa antas ng zero-rate. Kung gumagamit ka ng isang multimeter kailangan mong mapanatili ang isang pare-pareho na rate ng pag-ikot ng hindi bababa sa ilang segundo at tandaan ang boltahe sa pag-ikot na ito, pagkatapos ihambing ito sa boltahe ng zero-rate. Kung ito ay mas malaki kaysa sa zero-rate boltahe nangangahulugan ito na ang direksyon ng pag-ikot ay positibo.
Hakbang 3: Pagsasama-sama ng Accelerometer at Gyro
Pagsasama-sama ng lahat - Pagsasama-sama ng data ng accelerometer at gyroscope
Kung binabasa mo ang artikulong ito marahil ay nakuha mo o nagpaplano kang kumuha ng isang aparato ng IMU, o marahil ay nagpaplano kang bumuo ng isa mula sa magkakahiwalay na aparato ng accelerometer at gyroscope.
Ang unang hakbang sa paggamit ng isang kumbinasyon na aparato ng IMU na pinagsasama ang isang accelerometer at isang gyroscope ay upang ihanay ang kanilang mga coordinate system. Ang pinakamadaling paraan upang gawin ito ay upang piliin ang coordinate system ng accelerometer bilang iyong sanggunian na coordinate system. Ang karamihan sa mga sheet ng data ng accelerometer ay ipapakita ang direksyon ng X, Y, Z axes na may kaugnayan sa imahe ng pisikal na maliit na tilad o aparato. Halimbawa narito ang mga direksyon ng X, Y, Z axes tulad ng ipinakita sa mga pagtutukoy para sa Acc_Gyro board:
Ang mga susunod na hakbang ay:
Tukuyin ang mga output ng gyroscope na tumutugma sa mga halagang RateAxz, RateAyz na tinalakay sa itaas. Tukuyin kung ang mga output na ito ay kailangang baligtarin dahil sa pisikal na posisyon ng gyroscope na may kaugnayan sa accelerometer
Huwag ipagpalagay na kung ang isang gyroscope ay may output na minarkahang X o Y, ito ay tumutugma sa anumang axis sa accelerometer coordinate system, kahit na ang output na ito ay bahagi ng isang unit ng IMU. Ang pinakamahusay na paraan ay upang subukan ito. Ipagpalagay na naayos mo ang posisyon ng gyroscope na may kaugnayan sa accelerometer. Ipinapalagay na ang mga hangganan ng gyro at accelerometer ay magkatugma sa bawat isa, ibig sabihin inilalagay mo ang gyro sa isang anggulo ng maramihang 90deg na may kaugnayan sa chip ng accelerometer. Kung nakakuha ka ng isang board ng IMU ay malamang na nakahanay ang mga ito sa ganitong paraan. Hindi namin tatalakayin ang mga modelo ng artikulong ito kung saan ang gyroscope ay inilalagay sa isang hindi regular na anggulo na may kaugnayan sa accelerometer (sabihin nating 45 o 30 degree), kahit na ito ay maaaring maging kapaki-pakinabang sa ilang mga application.
Narito ang isang sample na pagkakasunud-sunod upang matukoy kung aling output ng gyroscope ang tumutugma sa halaga ng RateAxz na tinalakay sa itaas.
- Magsimula sa paglalagay ng aparato sa pahalang na posisyon. Ang parehong mga output ng X at Y ng accelerometer ay maglalabas ng zero-g boltahe (halimbawa para sa Acc_Gyro board na ito ay 1.65V)
- Susunod na simulang paikutin ang aparato sa paligid ng Y axis, isa pang paraan upang masabi na paikutin mo ang aparato sa XZ na eroplano, upang ang X at Z na output ng accelerometer ay nagbabago at ang Y output ay nananatiling pare-pareho. - habang umiikot ang aparato sa isang pare-parehong bilis ng tala kung aling mga pagbabago ng output ng gyroscope, ang iba pang mga output ng gyroscope ay dapat manatiling pare-pareho - ang output ng gyroscope na nagbago habang umiikot sa paligid ng Y axis (pag-ikot sa XZ na eroplano) ay magbibigay ng halaga ng pag-input para sa AdcGyroXZ, mula sa kung saan kinakalkula namin ang RateAxz - ang pangwakas na hakbang ay upang matiyak na ang direksyon ng pag-ikot ay tumutugma sa aming modelo, sa ilang mga kaso maaari mong baligtarin ang halaga ng RateAxz dahil sa pisikal na posisyon ng gyroscope na may kaugnayan sa accelerometer - gampanan muli ang pagsubok sa itaas, paikutin ang aparato ang Y axis, sa oras na ito subaybayan ang X output ng accelerometer (AdcRx sa aming modelo). Kung ang AdcRx ay lumalaki (ang unang 90 degree na pag-ikot mula sa pahalang na posisyon), pagkatapos ay dapat ding lumaki ang AdcGyroXZ. Kung hindi man kailangan mong baligtarin ang RateAxz, maaari mo itong makamit sa pamamagitan ng pagpapakilala ng isang kadahilanan ng pag-sign sa Eq.3, tulad ng sumusunod:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity, kung saan ang InvertAxz ay 1 o -1
ang parehong test cane ay tapos na para sa RateAyz, sa pamamagitan ng pag-ikot ng aparato sa paligid ng X axis, at maaari mong makilala kung aling output ng gyroscope ang tumutugma sa RateAyz, at kung kailangan itong baligtarin. Kapag mayroon ka ng halaga para sa InvertAyz, dapat mong gamitin ang sumusunod na formula upang makalkula ang RateAyz:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Sensitivity
Kung gagawin mo ang mga pagsubok na ito sa Acc_Gyro board makakakuha ka ng mga sumusunod na resulta:
- ang output pin para sa RateAxz ay GX4 at InvertAxz = -1. - ang output pin para sa RateAyz ay GY4 at InvertAyz = -1
Mula sa puntong ito isasaalang-alang namin na na-set up mo ang iyong IMU sa paraang maaari mong kalkulahin ang wastong mga halaga para sa Axr, Ayr, Azr (tulad ng tinukoy na Bahagi 1. Accelerometer) at RateAxz, RateAyz (tulad ng tinukoy sa Bahagi 2. Gyroscope). Susunod ay susuriin namin ang mga ugnayan sa pagitan ng mga halagang ito na magiging kapaki-pakinabang sa pagkuha ng mas tumpak na pagtantya sa pagkahilig ng aparato na may kaugnayan sa ground plan.
Maaari mong tanungin ang iyong sarili sa pamamagitan ng puntong ito, kung ang modelo ng accelerometer ay nagbigay sa amin ng mga anggulo ng pagkahilig ng Axr, Ayr, Azr bakit nais naming mag-abala sa data ng gyroscope? Ang sagot ay simple: ang data ng accelerometer ay hindi palaging mapagkakatiwalaang 100%. Mayroong maraming mga kadahilanan, tandaan na ang sukat ng sukat ng sukat ay sumusukat sa lakas na inertial, ang naturang puwersa ay maaaring sanhi ng gravitation (at perpekto lamang sa pamamagitan ng gravitation), ngunit maaaring sanhi din ito ng pagbilis (paggalaw) ng aparato. Bilang isang resulta kahit na ang accelerometer ay nasa isang matatag na estado, napaka-sensitibo pa rin ito sa panginginig ng boses at ingay ng mekanikal sa pangkalahatan. Ito ang pangunahing dahilan kung bakit ang karamihan sa mga sistema ng IMU ay gumagamit ng isang gyroscope upang makinis ang anumang mga error sa accelerometer. Ngunit paano ito nagagawa? At ang gyroscope ay libre mula sa ingay?
Ang gyroscope ay hindi malaya mula sa ingay gayunpaman dahil sinusukat nito ang pag-ikot ay hindi gaanong sensitibo sa mga paggalaw ng mekanikal na linear, ang uri ng ingay na naghihirap mula sa accelerometer, subalit ang mga gyroscope ay may iba pang mga uri ng mga problema tulad ng halimbawa ng naaanod (hindi babalik sa zero-rate na halaga kapag huminto ang pag-ikot). Gayunpaman sa pamamagitan ng pag-average ng data na nagmula sa accelerometer at gyroscope maaari kaming makakuha ng isang medyo mas mahusay na pagtatantya ng kasalukuyang pagkahilig ng aparato kaysa sa makukuha natin sa pamamagitan ng paggamit ng data ng accelerometer na nag-iisa.
Sa mga susunod na hakbang ay ipakilala ko ang isang algorithm na inspirasyon ng ilang mga ideya na ginamit sa Kalman filter, subalit sa mas simple at mas madaling ipatupad sa mga naka-embed na aparato. Bago iyon tingnan muna natin kung ano ang nais nating kalkulahin ng aming algorithm. Sa gayon, ito ang direksyon ng gravitation force vector R = [Rx, Ry, Rz] na kung saan maaari nating makuha ang iba pang mga halagang tulad ng Axr, Ayr, Azr o cosX, komportable, cosZ na magbibigay sa amin ng isang ideya tungkol sa pagkahilig ng aming aparato na may kaugnayan sa eroplano sa lupa, tinatalakay namin ang kaugnayan sa pagitan ng mga halagang ito sa Bahagi 1. Maaaring sabihin ng isa - wala na ba tayong mga halagang ito Rx, Ry, Rz mula sa Eq.2 sa Bahagi 1? Oo oo, ngunit tandaan na ang mga halagang ito ay nagmula lamang sa data ng accelerometer, kaya kung nais mong gamitin ang mga ito nang direkta sa iyong aplikasyon maaari kang makakuha ng mas maraming ingay kaysa sa maaaring tiisin ng iyong aplikasyon. Upang maiwasan ang karagdagang pagkalito ay tukuyin natin muli ang mga sukat ng accelerometer tulad ng sumusunod:
Ang Racc - ay ang inertial force vector na sinusukat ng accelerometer, na binubuo ng mga sumusunod na bahagi (pagpapakita sa X, Y, Z axes):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Sensitivity RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Sensitivity RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Sensitivity
Sa ngayon mayroon kaming isang hanay ng mga sinusukat na halaga na maaari naming makuha nang pulos mula sa mga halaga ng accelerometer ADC. Tatawagan namin ang hanay ng data na ito ng isang "vector" at gagamitin namin ang sumusunod na notasyon.
Racc = [RxAcc, RyAcc, RzAcc]
Dahil ang mga sangkap na ito ng Racc ay maaaring makuha mula sa data ng accelerometer, maaari naming isaalang-alang ito bilang isang input sa aming algorithm.
Mangyaring tandaan na dahil sinusukat ni Racc ang puwersa ng gravitation magiging tama ka kung ipinapalagay mong ang haba ng vector na ito na tinukoy tulad ng sumusunod ay pantay o malapit sa 1g.
| Racc | = SQRT (RxAcc ^ 2 + RyAcc ^ 2 + RzAcc ^ 2), Gayunpaman upang matiyak na makatuwiran na i-update ang vector na ito tulad ng sumusunod:
Racc (normalized) = [RxAcc / | Racc |, RyAcc / | Racc |, RzAcc / | Racc |].
Tiyakin nitong ang haba ng iyong na-normalize na Racc vector ay palaging 1.
Susunod ay magpapakilala kami ng isang bagong vector at tatawagin namin ito
Pahinga = [RxEst, RyEst, RzEst]
Ito ang magiging output ng aming algorithm, ang mga ito ay naitama na halaga batay sa data ng gyroscope at batay sa nakaraang tinatayang data.
Narito kung ano ang gagawin ng aming algorithm: - Sinasabi sa amin ng accelerometer: "Nasa posisyon ka na ngayon Racc" - sinasabi namin na "Salamat, ngunit hayaan mong suriin ko", - pagkatapos ay iwasto ang impormasyong ito sa data ng gyroscope pati na rin sa nakaraang data ng Pahinga at naglalabas kami ng isang bagong tinatayang vector Rest. - Isinasaalang-alang namin ang Pahinga na aming "pinakamahusay na mapagpipilian" tungkol sa kasalukuyang posisyon ng aparato.
Tingnan natin kung paano natin ito maisasagawa.
Sisimulan namin ang aming pagkakasunud-sunod sa pamamagitan ng pagtitiwala sa aming accelerometer at pagtatalaga ng:
Pahinga (0) = Racc (0)
Sa pamamagitan ng alaala tandaan ang Rest at Racc ay mga vector, kaya ang equation sa itaas ay isang simpleng paraan lamang upang magsulat ng 3 mga hanay ng mga equation, at maiwasan ang pag-uulit:
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
Susunod na gagawin namin ang regular na pagsukat sa pantay na agwat ng oras ng T segundo, at makakakuha kami ng mga bagong sukat na tutukuyin namin bilang Racc (1), Racc (2), Racc (3) at iba pa. Maglabas din kami ng mga bagong pagtatantya sa bawat oras na agwat ng Pahinga (1), Pahinga (2), Pahinga (3) at iba pa.
Ipagpalagay na nasa hakbang kami n. Mayroon kaming dalawang kilalang hanay ng mga halagang nais naming gamitin:
Pahinga (n-1) - ang aming dating pagtatantya, na may Pahinga (0) = Racc (0) Racc (n) - ang aming kasalukuyang pagsukat ng accelerometer
Bago namin makalkula ang Rest (n), ipakilala natin ang isang bagong sinusukat na halaga, na maaari nating makuha mula sa aming gyroscope at isang nakaraang pagtatantya.
Tatawagin namin itong Rgyro, at ito rin ay isang vector na binubuo ng 3 bahagi:
Rgyro = [RxGyro, RyGyro, RzGyro]
Kalkulahin namin ang vector na ito ng isang bahagi nang paisa-isa. Magsisimula kami sa RxGyro.
Magsimula tayo sa pamamagitan ng pagmamasid sa sumusunod na ugnayan sa aming modelo ng gyroscope, mula sa kanang sulok na tatsulok na nabuo ni Rz at Rxz maaari nating makuha iyon:
tan (Axz) = Rx / Rz => Axz = atan2 (Rx, Rz)
Ang Atan2 ay maaaring isang pagpapaandar na hindi mo nagamit dati, katulad ito sa atan, maliban kung nagbabalik ng mga halagang saklaw ng (-PI, PI) na taliwas sa (-PI / 2, PI / 2) na ibinalik ng atan, at kinakailangan 2 mga argumento sa halip na isa. Pinapayagan kaming i-convert ang dalawang halaga ng Rx, Rz sa mga anggulo sa buong saklaw ng 360 degree (-PI hanggang PI). Maaari kang magbasa nang higit pa tungkol sa atan2 dito.
Kaya alam ang RxEst (n-1), at RzEst (n-1) maaari nating hanapin:
Axz (n-1) = atan2 (RxEst (n-1), RzEst (n-1)).
Tandaan na sinusukat ng gyroscope ang rate ng pagbabago ng anggulo ng Axz. Maaari nating tantyahin ang bagong anggulo ng Axz (n) tulad ng sumusunod:
Axz (n) = Axz (n-1) + RateAxz (n) * T
Tandaan na ang RateAxz ay maaaring makuha mula sa aming mga pagbabasa ng gyroscope ADC. Ang isang mas tumpak na formula ay maaaring gumamit ng average na rate ng pag-ikot na kinakalkula bilang mga sumusunod:
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
Ang parehong paraan na maaari naming hanapin:
Ayz (n) = Ayz (n-1) + RateAyz (n) * T
Ok kaya ngayon mayroon kaming Axz (n) at Ayz (n). Saan tayo pupunta mula dito upang ibawas ang RxGyro / RyGyro? Mula sa Eq Maaari nating isulat ang haba ng vector Rgyro tulad ng sumusunod:
| Rgyro | = SQRT (RxGyro ^ 2 + RyGyro ^ 2 + RzGyro ^ 2)
Gayundin dahil na-normalize namin ang aming Racc vector, maaari naming ipalagay na ang haba nito ay 1 at hindi ito nagbago pagkatapos ng pag-ikot, kaya't ligtas itong magsulat:
| Rgyro | = 1
Magpatibay tayo ng isang pansamantalang mas maikling notasyon para sa mga kalkulasyon sa ibaba:
x = RxGyro, y = RyGyro, z = RzGyro
Gamit ang mga ugnayan sa itaas maaari naming isulat:
x = x / 1 = x / SQRT (x ^ 2 + y ^ 2 + z ^ 2)
Hatiin natin ang numerator at denominator ng maliit na bahagi sa pamamagitan ng SQRT (x ^ 2 + z ^ 2)
x = (x / SQRT (x ^ 2 + z ^ 2)) / SQRT ((x ^ 2 + y ^ 2 + z ^ 2) / (x ^ 2 + z ^ 2))
Tandaan na x / SQRT (x ^ 2 + z ^ 2) = sin (Axz), kaya:
x = sin (Axz) / SQRT (1 + y ^ 2 / (x ^ 2 + z ^ 2))
Ngayon paramihin ang numerator at denominator ng maliit na bahagi sa loob ng SQRT ng z ^ 2
x = sin (Axz) / SQRT (1 + y ^ 2 * z ^ 2 / (z ^ 2 * (x ^ 2 + z ^ 2)))
Tandaan na z / SQRT (x ^ 2 + z ^ 2) = cos (Axz) at y / z = tan (Ayz), kaya sa wakas:
x = sin (Axz) / SQRT (1 + cos (Axz) ^ 2 * tan (Ayz) ^ 2)
Bumabalik sa aming notasyon nakukuha namin:
RxGyro = sin (Axz (n)) / SQRT (1 + cos (Axz (n)) ^ 2 * tan (Ayz (n)) ^ 2)
sa parehong paraan nahanap natin iyon
RyGyro = sin (Ayz (n)) / SQRT (1 + cos (Ayz (n)) ^ 2 * tan (Axz (n)) ^ 2)
Ngayon, sa wakas mahahanap natin ang:
RzGyro = Mag-sign (RzGyro) * SQRT (1 - RxGyro ^ 2 - RyGyro ^ 2).
Kung saan Mag-sign (RzGyro) = 1 kapag RzGyro> = 0, at Mag-sign (RzGyro) = -1 kapag RzGyro <0.
Ang isang simpleng paraan upang matantya ito ay ang kumuha ng:
Mag-sign (RzGyro) = Mag-sign (RzEst (n-1))
Sa pagsasanay, mag-ingat kapag ang RzEst (n-1) ay malapit sa 0. Maaari mong laktawan ang yugto ng gyro sa kasong ito at magtalaga ng: Rgyro = Rest (n-1). Ginagamit ang Rz bilang isang sanggunian para sa pagkalkula ng mga anggulo ng Axz at Ayz at kapag malapit ito sa 0, ang mga halaga ay maaaring mag-oveflow at magpalitaw ng hindi magagandang resulta. Malalagay ka sa domain ng malalaking mga lumulutang na numero ng numero kung saan maaaring kulang sa katumpakan ang pagpapatupad ng pag-andar ng tan () / atan ().
Kaya't ulitin natin kung ano ang mayroon tayo, nasa hakbang tayo ng aming algorithm at kinakalkula namin ang mga sumusunod na halaga:
Racc - kasalukuyang mga pagbabasa mula sa aming accelerometer Rgyro - nakuha mula sa Pahinga (n-1) at kasalukuyang pagbasa ng gyroscope
Aling mga halaga ang ginagamit namin upang makalkula ang na-update na tantyahin na Rest (n)? Marahil nahulaan mo na gagamitin namin ang pareho. Gumagamit kami ng isang timbang na average, upang:
Pahinga (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Maaari nating gawing simple ang formula na ito sa pamamagitan ng paghati sa parehong numerator at denominator ng maliit na bahagi ng w1.
Pahinga (n) = (Racc * w1 / w1 + Rgyro * w2 / w1) / (w1 / w1 + w2 / w1)
at pagkatapos ng pagpapalit ng w2 / w1 = wGyro nakukuha natin:
Pahinga (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
Sa itaas na forumula sinabi sa amin ng wGyro kung gaano kami nagtitiwala sa aming gyro kumpara sa aming accelerometer. Ang halagang ito ay maaaring mapili nang eksperimento karaniwang mga halaga sa pagitan ng 5..20 ay mag-uudyok ng magagandang resulta.
Ang pangunahing pagkakaiba ng algorithm na ito mula sa Kalman filter ay ang timbang na ito ay medyo naayos, samantalang sa filter ng Kalman ang mga timbang ay permanenteng na-update batay sa sinusukat na ingay ng mga pagbasa ng accelerometer. Ang filter ng Kalman ay nakatuon sa pagbibigay sa iyo ng "pinakamahusay na" mga resulta ng teoretikal, samantalang ang algorithm na ito ay maaaring magbigay sa iyo ng mga resulta na "sapat na mabuti" para sa iyong praktikal na aplikasyon. Maaari kang magpatupad ng isang algorithm na inaayos ang wGyro depende sa ilang mga kadahilanan ng ingay na iyong sinusukat, ngunit ang mga nakapirming halaga ay gagana nang maayos para sa karamihan ng mga application.
Kami ay isang hakbang ang layo mula sa pagkuha ng aming na-update na tinantyang mga halaga:
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Ngayon ay gawing normal natin ang vector na ito:
R = SQRT (RxEst (n) ^ 2 + RyEst (n) ^ 2 + RzEst (n) ^ 2)
RxEst (n) = RxEst (n) / R RyEst (n) = RyEst (n) / R RzEst (n) = RzEst (n) / R
At handa na kaming ulitin muli ang aming loop.
Ang gabay na ito ay orihinal na lumitaw sa starlino.com, gumawa ako ng kaunting mga pag-edit at muling nai-post ito nang may pahintulot. Salamat Starlino!
Inirerekumendang:
MPU 6050 Gyro, Komunikasyon ng Accelerometer Sa Arduino (Atmega328p): 5 Mga Hakbang
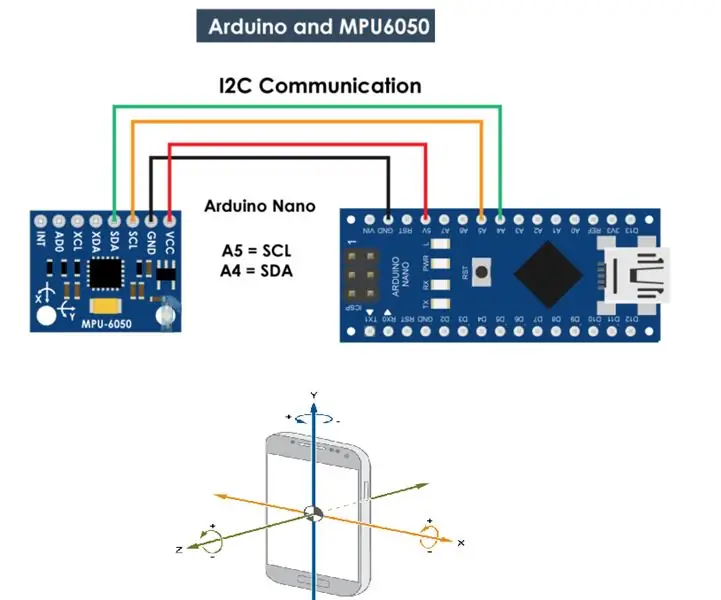
Ang MPU 6050 Gyro, Komunikasyon ng Accelerometer Sa Arduino (Atmega328p): Ang MPU6050 IMU ay may parehong 3-Axis accelerometer at 3-Axis gyroscope na isinama sa isang solong maliit na tilad. Sinusukat ng gyroscope ang bilis ng pag-ikot o rate ng pagbabago ng angular na posisyon sa paglipas ng panahon, kasama ang X, Y at Z axis. Ang mga output ng gyroscope ar
Arduino Nano - MMA8452Q 3-Axis 12-bit / 8-bit Digital Accelerometer Tutorial: 4 Mga Hakbang

Arduino Nano - MMA8452Q 3-Axis 12-bit / 8-bit Digital Accelerometer Tutorial: Ang MMA8452Q ay isang matalino, mababang lakas, three-axis, capacitive, micromachined accelerometer na may 12 piraso ng resolusyon. Ang mga nababaluktot na pagpipilian na maaaring mai-program ng gumagamit ay ibinibigay sa tulong ng mga naka-embed na pag-andar sa accelerometer, mai-configure sa dalawang nakakagambala
Raspberry Pi MMA8452Q 3-Axis 12-bit / 8-bit Digital Accelerometer Python Tutorial: 4 Mga Hakbang

Raspberry Pi MMA8452Q 3-Axis 12-bit / 8-bit Digital Accelerometer Python Tutorial: Ang MMA8452Q ay isang matalino, mababang lakas, three-axis, capacitive, micromachined accelerometer na may 12 piraso ng resolusyon. Ang mga nababaluktot na pagpipilian na maaaring mai-program ng gumagamit ay ibinibigay sa tulong ng mga naka-embed na pag-andar sa accelerometer, mai-configure sa dalawang nakakagambala
Xbox 360 Controller Accelerometer / gyro Steering Mod: 7 Mga Hakbang

Xbox 360 Controller Accelerometer / gyro Steering Mod: Naglalaro ako ng Assetto Corsa kasama ang aking Xbox 360 controller. Sa kasamaang palad, ang pagpipiloto gamit ang analogue stick ay napaka-mahirap, at wala akong puwang para sa isang pag-set up ng gulong. Sinubukan kong mag-isip ng mga paraan kung paano ko mailalagay ang isang mas mahusay na mekanismo ng pagpipiloto sa
Pagsukat ng Angle Gamit ang Gyro, Accelerometer at Arduino: 5 Hakbang

Pagsukat ng Angle Paggamit ng Gyro, Accelerometer at Arduino: Ang aparato ay isang magaspang na prototype ng kung ano sa paglaon ay magiging isang self balanse robot, ito ang pangalawang bahagi ng butas na bagay (basahin ang accelerometer at kontrolin ang isang motor sa balanse ng sarili). Ang unang bahagi na may gyro lamang ay matatagpuan dito. Sa ganitong pagkakataon
